如图,已知BD平分∠ABF,且交AE于点D,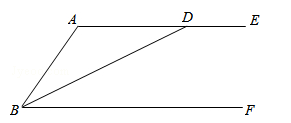
(1)求作:∠BAE的平分线AP(要求:尺规作图,保留作图痕迹,不写作法);
(2)设AP交BD于点O,交BF于点C,连接CD,当AC⊥BD时,求证:四边形ABCD是菱形.
如图,菱形ABCD,四个顶点分别是A(-2,1),B(1,-3),C(4,-1),D(1,1).将菱形沿x轴负方向平移3个单位长度,各个顶点的坐标变为多少?将它沿y轴正方向平移4个单位长度呢?分别画出平移后的图形.
在平面直角坐标系中,△ABC的边AB在x轴上,且AB=3,顶点A的坐标为(-5,0),顶点C的坐标为(2,5).
(1).画出所有符合条件的△ABC,并直接写出点B的坐标.
(2).求△ABC的面积.
如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.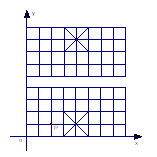
⑴写出下一步“马”可能到达的点的坐标 ;
⑵顺次连接⑴中的所有点,得到的图形是 图形(填“中心对称”、“旋转对称”、“轴对称”);
⑶指出⑴中关于点P成中心对称的点 .
如图,在所给的坐标系中描出下列各点的位置:
A(-4,4) B(-2,2) C(3,-3)
D(5,-5) E(-3,3) F(0,0)
你发现这些点有什么关系?你能再找出一些类似的点吗?
在平面直角坐标系中,画出点A(0,2),B(-1,0),过点A作直线L1∥x轴,过点B作L2∥y轴,分析L1,L2上点的坐标特点,由此,你能总结出什么规律?