某工厂通过科技创新,生产效率不断提高.已知去年月平均生产量为120台机器,今年一月份的生产量比去年月平均生产量增长了m%,二月份的生产量又比一月份生产量多50台机器,而且二月份生产60台机器所需要时间与一月份生产45台机器所需时间相同,三月份的生产量恰好是去年月平均生产量的2倍.
问:今年第一季度生产总量是多少台机器?m的值是多少?
某小区超市一段时间每天订购80个面包进行销售,每售出1个面包获利润0.5元,未售出的每个亏损0.3元.(1)若今后每天售出的面包个数用x(0<x≤80)表示,每天销售面包的利润用y(元)表示,写出y与x的函数关系式;
(2)小明连续m天对该超市的面包销量进行统计,并制成了频数分别直方图(每个组距包含左边的数,但不包含右边的数)和扇形统计图,如图1、图2所示,请结合两图提供的信息,解答下列问题:
①m的值为 ;
②求在m天内日销售利润少于32元的天数;
(3)如图(2)中m天内日销售面包个数在70≤x<80这个组内的销售情况如表:
| 销售量/个 |
70 |
72 |
73 |
75 |
78 |
79 |
| 天数 |
1 |
2 |
3 |
4 |
3 |
2 |
请计算该组内平均每天销售面包的个数.
已知一元二次方程ax2+2x-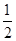 =0有唯一的解,求
=0有唯一的解,求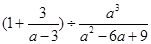 的值.
的值.
抛物线与x轴交于A,B两点,(点B在点A的左侧)且A,B两点的坐标分别为(-2,0)、(8,0),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线L交抛物线于点Q,交BD于点M.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,试探究m为何值时,四边形CQMD是平行四边形?
(3)在(2)的结论下,试问抛物线上是否存在点N(不同于点Q),使三角形BCN的面积等于三角形BCQ的面积?若存在,请求出点N的坐标;若不存在,请说明理由.
如图,已知AB,AC分别是⊙O的直径和弦,D为优弧AC上的一点,ED为⊙O的一条弦,交AB于点H,交AC于点F,过点C画⊙O的切线交ED的延长线于点P,且PC=PF.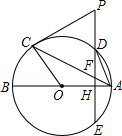
(1)求证:AB⊥ED;
(2)当点D为优弧AC的中点时,连接AD,若DF=3、AD=4,求EF的长及sin∠BED的值.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.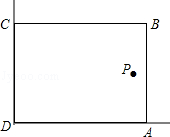
(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.