抛物线与x轴交于A，B两点，（点B在点A的左侧）且A，B两点的坐标分别为（-2，0）、（8，0），与y轴交于点C，连接BC，以BC为一边，点O为对称中心作菱形BDEC，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线L交抛物线于点Q，交BD于点M．
（1）求抛物线的解析式；
（2）当点P在线段OB上运动时，试探究m为何值时，四边形CQMD是平行四边形？
（3）在（2）的结论下，试问抛物线上是否存在点N（不同于点Q），使三角形BCN的面积等于三角形BCQ的面积？若存在，请求出点N的坐标；若不存在，请说明理由．
在△ABC中，∠ACB=2∠B，（1）如图①，当∠C=90°，AD为∠ABC的角平分线时，在AB上截取AE=AC，连接DE，易证AB=AC+CD．请证明AB=AC+CD；
（2）①如图②，当∠C≠90°，AD为∠BAC的角平分线时，线段AB、AC、CD又有怎样的数量关系？请直接写出你的结论，不要求证明；
②如图③，当∠C≠90°，AD为△ABC的外角平分线时，线段AB、AC、CD又有怎样的数量关系？请写出你的猜想并证明．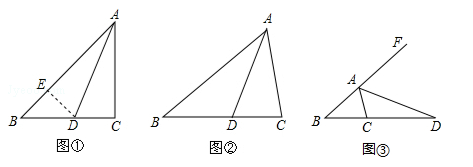
阅读材料，回答下列问题：
我们知道对于二次三项式
这样的完全平方式，可以用公式将它分解成
的形式，但是，对于二次三项式
就不能直接用完全平方公式，可以采用如下方法：
＝
＝
．
像上面这样把二次三项式分解因式的数学方法是配方法．请同学们借助这种数学思想方法把多项式
分解因式．
如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．
求证：（1）△AEF≌△CEB；（2）AF=2CD．
因式分解
（1）
（2）
（3）
（4）
（5）
（6）
如图，抛物线经过A（
，0），B（
，0），C（0，2）三点．
（1）求抛物线的解析式；
（2）在直线AC下方的抛物线上有一点D，使得△DCA的面积最大，求点D的坐标；
（3）设点M是抛物线的顶点，试判断抛物线上是否存在点H满足
？若存在，请求出点H的坐标；若不存在，请说明理由．