如图,在平面直角坐标系中,四边形OABC的O点为坐标原点,A、C两点分别在y轴和x轴上,AB∥OC,OA=8,AB=24,OC=26,动点P从A开始沿AB边向点D以1个单位/s的速度运动,动点Q从C开始沿CO边向点O以3个单位/s的速度运动,P、Q分别从A、C同时出发,当一点到达时另一点也停止,设运动时间为t.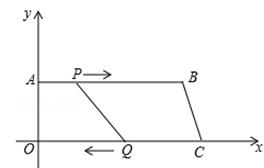
(1)求直线BC的解析式;
(2)当t为何值时,PQ∥CB?
(3)是否存在t的值,使得PQ将四边形OABC的面积分成2:3两部分?若存在,求出t的值;若不存在,请说明理由.
先化简,再求值: ,其中
,其中 .
.
(1)计算: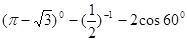 ;
;
(2)解分式方程: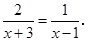
(本题10分)如图1,矩形ABCD中,点P从A出发,以3cm/s的速度沿边A→B→C→D→A匀速运动;同时点Q从B出发,沿边B→C→D匀速运动,当其中一个点到达终点时两点同时停止运动,设点P运动的时间为t s.△APQ的面积s(cm2)与t(s)之间函数关系的部分图像由图2中的曲线段OE与线段EF给出.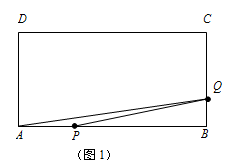
(1)点Q运动的速度为cm/s,a﹦cm2;
(2)若BC﹦3cm,① 求t>3时S的函数关系式;② 在图(2)中画出①中相应的函数图像.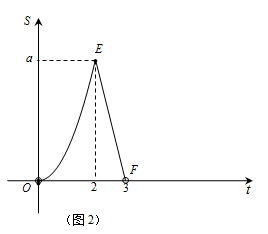
动手实验:利用矩形纸片(图1)剪出一个正六边形纸片;利用这个正六边形纸片做一个如图(2)无盖的正六棱柱(棱柱底面为正六边形);
(1)做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少?
(2)在(1)的前提下,当矩形的长为2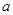 时,要使无盖正六棱柱侧面积最大,正六棱柱的高为多少?并求此时矩形纸片的利用率?(矩形纸片的利用率=
时,要使无盖正六棱柱侧面积最大,正六棱柱的高为多少?并求此时矩形纸片的利用率?(矩形纸片的利用率= 无盖正六棱柱的表面积/矩形纸片的面积)
无盖正六棱柱的表面积/矩形纸片的面积)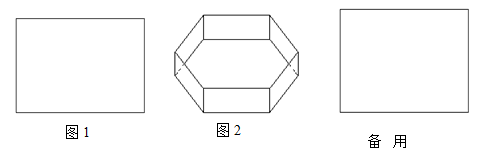
某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.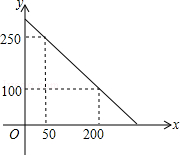
(1)根据图象,求y与x之间的函数关系式;
(2)求甲、乙两种品牌的文具盒进货单价;
(3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?