水利部确定每年的3月22日至28日为“中国水周”（1994年以前为7月1日至7日），从1991年起，我国还将每年5月的第二周作为城市节约用水宣传周．某社区为了进一步提高居民珍惜水、保护水和水忧患意识，提倡节约用水，从本社区5000户家庭中随机抽取100户，调查他们家庭每月的平均用水量，并将调查的结果绘制成如下的两幅不完整的统计图表：
请根据上面的统计图表，解答下列问题：
（1）在频数分布表中：m= ，n= ；
（2）根据题中数据补全频数直方图；
（3）如果自来水公司将基本月用水量定为每户每月12吨，不超过基本月用水量的部分享受基本价格，超出基本月用水量的部分实行加价收费，那么该社区用户中约有多少户家庭能够全部享受基本价格？
据报载，在“百万家庭低碳行，垃圾分类要先行”活动中，某地区对随机抽取的1000名公民的年龄段分布情况和对垃圾分类所持态度进行调查，并将调查结果分别绘成条形图（图①）、扇形图（图②）．
（1）图2中所缺少的百分数是____________；
（2）这次随机调查中，如果公民年龄的中位数是正整数，那么这个中位数所在年龄段是______（填写年龄段）；
（3）这次随机调查中，年龄段是“25岁以下”的公民中“不赞成”的有5名，它占“25岁以下”人数的百分数是_____________；
（4）如果把所持态度中的“很赞同”和“赞同”统称为“支持”，那么这次被调查公民中“支持”的人有___________名．
如图，已知矩形ABCD中，E是AD上的一点，F是AB上的一点，EF⊥EC，且EF=EC，DE=4cm，矩形ABCD的周长为32cm，求AE的长．
（1）解方程：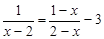
；（2）解不等式组：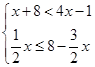
计算或化简：
（1）计算：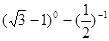
＋|2−3|＋sin245°
（2）先化简，再求值：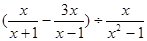
，其中x＝－2.
操作：在△ABC中，AC＝BC＝2，∠C＝90°，将一块等腰直角三角板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点（不包括射线的端点）.如图1，2，3是旋转三角板得到的图形中的3种情况.
研究：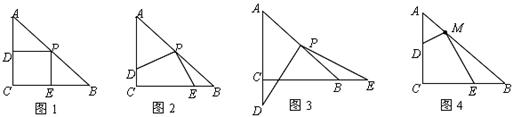
（1）三角板绕点P旋转，观察线段PD和PE之间有什么数量关系？并结合如图2加以证明；
（2）三角板绕点P旋转，△PBE是否能成为等腰三角形？若能，指出所有情况（即写出△PBE为等腰三角形时CE的长；若不能，请说明理由；
（3）若将三角板的直角顶点放在斜边AB上的M处，且AM∶MB＝1∶3，和前面一样操作，试问线段MD和ME之间有什么数量关系？并结合如图4加以证明.