如图,二次函数 的图象交x轴于A(﹣1,0)、B(3,0)两点,交y轴于点C,连接BC,动点P以每秒1个单位长度的速度从A向B运动,动点Q以每秒
的图象交x轴于A(﹣1,0)、B(3,0)两点,交y轴于点C,连接BC,动点P以每秒1个单位长度的速度从A向B运动,动点Q以每秒 个单位长度的速度从B向C运动,P、Q同时出发,连接PQ,当点Q到达C点时,P、Q同时停止运动,设运动时间为t秒.
个单位长度的速度从B向C运动,P、Q同时出发,连接PQ,当点Q到达C点时,P、Q同时停止运动,设运动时间为t秒.
(1)求二次函数的解析式;
(2)如图1,当△BPQ为直角三角形时,求t的值;
(3)如图2,当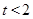 时,延长QP交y轴于点M,在抛物线上是否存在一点N,使得PQ的中点恰为MN的中点?若存在,求出点N的坐标与t的值;若不存在,请说明理由.
时,延长QP交y轴于点M,在抛物线上是否存在一点N,使得PQ的中点恰为MN的中点?若存在,求出点N的坐标与t的值;若不存在,请说明理由.
计算:(π-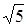 )0+
)0+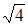 +(-1)2015-
+(-1)2015-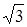 tan60°.
tan60°.
(北海)如图1所示,已知抛物线 的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
(1)直接写出D点和E点的坐标;
(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,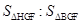 =5:6?
=5:6?
(3)图2所示的抛物线是由 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
(北海)如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
(百色)抛物线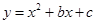 经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.
经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.
(1)求抛物线与x轴的交点坐标;
(2)若点C为抛物线与x轴的交点,是否存在点D,使A、B、C、D四点围成的四边形是平行四边形?若存在,求点D的坐标;若不存在,说明理由;
(3)问几秒钟时,B、D、E在同一条直线上?
(百色)已知⊙O为△ABC的外接圆,圆心O在AB上.
(1)在图1中,用尺规作图作∠BAC的平分线AD交⊙O于D(保留作图痕迹,不写作法与证明);
(2)如图2,设∠BAC的平分线AD交BC于E,⊙O半径为5,AC=4,连接OD交BC于F.
①求证:OD⊥BC;
②求EF的长.