我们把焦点相同，且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”．已知
是一对相关曲线的焦点，
是椭圆和双曲线在第一象限的交点，当
时，这一对相关曲线中椭圆的离心率为（ ）
A． |
B． |
C． |
D． |
下列函数中值域为正实数的是( )
| A．y＝－5x | B． |
C．y＝ |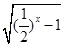
D． |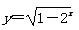
设a，b，c为实数，
.记集合S=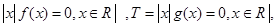
若cardS,cardT分别为集合元素S，T的元素个数，则下列结论不可能的是（）
（A）cardS=1, cardT=0（B）cardS=1, cardT=1
（C）cardS=2, cardT=2（D cardS="2," cardT=3
已知以F1(－2,0)，F2(2,0)为焦点的椭圆与直线x＋y＋4＝0有且仅有一个交点，则椭圆的长轴长为( )
| A．3 | B．2 | C．2 | D．4 |
设斜率为2的直线l过抛物线y2＝ax(a≠0)的焦点F，且和y轴交于点A，若△OAF(O为坐标原点)的面积为4，则抛物线的方程为( )
| A．y2＝±4x | B．y2＝±8 |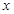
C．y2＝4x | D．y2＝8x |
f(x)是定义在(0，＋∞)上的非负可导函数，且满足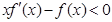
，对任意正数a，b，若a<b，则必有( )
| A．af(b)＜bf(a) | B．bf(a) ＜af(b) | C．af(a)＜bf (b) | D．bf(b) ＜a f(a) |