如图,在△ABC中,AB=AC,点D在边AB上,以点A为圆心,线段AD的长为半径的⊙A与边AC相交于点E,AF⊥DE,垂足为点F,AF的延长线与边BC相交于点G,联结GE.已知DE=10,cos∠BAG= ,
, .求:
.求:
(1)⊙A的半径AD的长;
(2)∠EGC的余切值.
如图,在平面直角坐标系中,⊙O的圆心在坐标原点,半径为3.过A(-7,9),B(0,9)的抛物线 (a,b,c为常数,且a≠0)与x轴交于D,E (点D在点E右边)两点,连结AD.
(a,b,c为常数,且a≠0)与x轴交于D,E (点D在点E右边)两点,连结AD.
(1)若点D的坐标为D(3,0).①请直接写出此时直线AD与⊙O的位置关系;②求此时抛物线对应的函数关系式;
(2)若直线AD和⊙O相切,求抛物线二次项系数a的值;
(3)当直线AD和⊙O相交时,直接写出a的取值范围.
(1)如图22-1,等腰Rt△ABO放在平面直角坐标系中, 点A,B 的坐标分别是A(0,1),B(1,0).在x轴正半轴上取D(m,0),在AD右上方作等腰Rt△ADE,∠ADE= .
.
①求出E点的坐标(可用含m的代数式表示);
②证明对于任意正数m,点E都在直线 上;
上;
(2)将(1)中的两个等腰直角三角形都改为有一个角为 的直角三角形,如图22-2,A(0,
的直角三角形,如图22-2,A(0, ),B(1,0).Rt△ADE中, ∠ADE=
),B(1,0).Rt△ADE中, ∠ADE= ,∠AED=
,∠AED= .D(m,0)是x轴正半轴上任意一点,则不论m取何正数,点E都在某一条直线上,请求出这条直线的函数关系式;
.D(m,0)是x轴正半轴上任意一点,则不论m取何正数,点E都在某一条直线上,请求出这条直线的函数关系式;
(3)将(2)中Rt△AOB保持不动,取点C(2,  ),在x轴正半轴上取D(m,0)(m>2), 然后在AD右上方作Rt△CDE, ∠CDE=
),在x轴正半轴上取D(m,0)(m>2), 然后在AD右上方作Rt△CDE, ∠CDE= ,∠CED=
,∠CED= .当m取不同值时,点E是否还是总在一条直线上? 若是,请求出直线对应的函数关系式,若不是,请说明理由.
.当m取不同值时,点E是否还是总在一条直线上? 若是,请求出直线对应的函数关系式,若不是,请说明理由.
如图,海边有两个灯塔A,B.即将靠岸的轮船得到信息:海里有一个以AB为弦的弓形暗礁区域,要求轮船在行驶过程中,对两灯塔的张角不能超过 .当轮船航行到P点时,测得轮船对两灯塔的张角∠APB刚好等于
.当轮船航行到P点时,测得轮船对两灯塔的张角∠APB刚好等于 .
.
(1)请用直尺和圆规在图中作出△APB的外接圆 (作出图形,不写作法,保留痕迹);
(2)若此时轮船到B的距离PB为700米,已知AB=500米,求出此时轮船到A的距离.
一次函数 (
(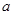 为常数,且
为常数,且 ).
).
(1)若点 在一次函数
在一次函数 的图象上,求
的图象上,求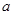 的值;
的值;
(2)当 时,函数有最大值2,请求出
时,函数有最大值2,请求出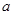 的值.
的值.
如图,在四边形ABCD中,AD∥BC, AB=AC,BE=CE=AD.
(1)求证:四边形ECDA是矩形;
(2)当△ABC是什么类型的三角形时,四边形ECDA是正方形?请说明理由.