某种盆栽花卉每盆的盈利与每盆种植花卉的株数有关:已知每盆种植3株时,平均每株可盈利4元;若每盆多种植1株,则平均每株盈利要减少0.5元.为使每盆的盈利达到15元,则每盆应种植花卉多少株?
如图,直线y=﹣x+3与x轴,y轴分别交于B,C两点,抛物线y=﹣x2+bx+c经过B,C两点,点A是抛物线与x轴的另一个交点.
(1)求B、C两点坐标;
(2)求此抛物线的函数解析式;
(3)在抛物线上是否存在点P,使S△PAB=S△CAB,若存在,求出P点坐标,若不存在,请说明理由.
如图,△ABC内接于⊙O,AB是⊙O的直径,C是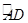 的中点,弦CE⊥AB于点H,连结AD,分别交CE、BC于点P、Q,连结BD
的中点,弦CE⊥AB于点H,连结AD,分别交CE、BC于点P、Q,连结BD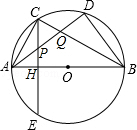
(1)求证:∠ACH=∠CBD;
(2)求证:P是线段AQ的中点;
(3)若⊙O 的半径为5,BH=8,求CE的长.
当a>0且x>0时,因为 ≥0,所以
≥0,所以 ≥0,从而
≥0,从而 (当
(当 时取等号).记函数
时取等号).记函数 ,由上述结论可知:当
,由上述结论可知:当 时,该函数有最小值为
时,该函数有最小值为 .
.
(1)已知函数y1=x(x>0)与函数 ,则当x= 1 时,y1+y2取得最小值为2 .
,则当x= 1 时,y1+y2取得最小值为2 .
(2)已知函数y1=x+1(x>﹣1)与函数 ,求
,求 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.
已知二次函数的图象经过点(0,3),顶点坐标为(1,4),
(1)求这个二次函数的解析式;
(2)求图象与x轴交点A、B两点的坐标;
(3)图象与y轴交点为点C,求三角形ABC的面积.