如图,在平面直角坐标系中.顶点为(﹣4,﹣1)的抛物线交y轴于点A(0,3),交x轴于B,C两点.
(1)求此抛物线的解析式;
(2)已知点P是抛物线上位于B,C两点之间的一个动点,问:当点P运动到什么位置时,四边形ABPC的面积最大?并求出此时四边形ABPC的面积.
(3)过点B作AB的垂线交抛物线于点D,是否存在以点C为圆心且与线段BD和抛物线的对称轴l同时相切的圆?若存在,求出圆的半径;若不存在,请说明理由.
在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为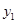 、
、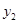 (km),
(km),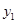 、
、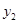 与x的函数关系如图所示.
与x的函数关系如图所示.
(1)填空:A、C两港口间的距离为km, ;
;
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)甲、乙两船同在行驶途中,若两船距离不超过10 km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.
(1)证明:不论 取什么值,直线
取什么值,直线 :y=
:y= x-
x- 都通过一个定点;
都通过一个定点;
(2)以A(0,2)、B(2,0)、O(0,0)为顶点的三角形被直线 分成两部分,分别求出当
分成两部分,分别求出当 =2和
=2和 =-
=-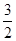 时,靠近原点O一侧的那部分面积.
时,靠近原点O一侧的那部分面积.
如图,AD=BC,AC=BD,AC、BD相交于O,求证:AB∥CD.
已知A=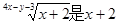 的算术平方根,B=
的算术平方根,B=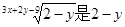 的立方根,求A+B的立方根.
的立方根,求A+B的立方根.
已知: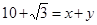 ,其中
,其中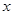 是整数,且
是整数,且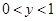 ,求
,求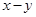 的相反数.
的相反数.