二次函数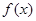 的图像顶点为
的图像顶点为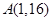 ,且图象在
,且图象在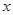 轴上截得线段长为
轴上截得线段长为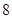 .
.
(1)求函数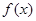 的解析式;
的解析式;
(2)令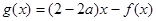
①若函数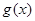 在
在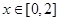 上是单调增函数,求实数
上是单调增函数,求实数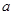 的取值范围;
的取值范围;
②求函数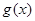 在
在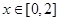 的最小值.
的最小值.
已知函数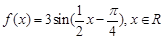 .
.
(1)列表并画出函数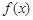 在长度为一个周期的闭区间上的简图;
在长度为一个周期的闭区间上的简图;
(2)将函数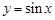 的图象作怎样的变换可得到
的图象作怎样的变换可得到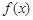 的图象?
的图象?
已知椭圆C: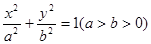 的两个焦点为F1、F2,点P在椭圆C上,且|PF1|=
的两个焦点为F1、F2,点P在椭圆C上,且|PF1|=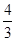 ,
,
|PF2|=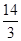 , PF1⊥F1F2.
, PF1⊥F1F2.
(1)求椭圆C的方程;(6分)
(2)若直线L过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程.
若函数f(x)=ax3-bx+4,当x=2时,函数f(x)有极值-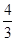 .
.
(1)求函数的解析式.
(2)若方程f(x)=k有3个不同的根,求实数k的取值范围.
用平行于棱锥底面的平面去截棱锥,则截面与底面之间的部分叫棱台。
如图,在四棱台 中,下底
中,下底 是边长为
是边长为 的正方形,上底
的正方形,上底 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱 ⊥平面
⊥平面 ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求平面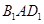 与平面
与平面 夹角的余弦值.
夹角的余弦值.
如图所示,在边长为60 cm的正方形铁片的四角上切去相等的正方形,再把它沿虚线折起,做成一个无盖的长方体箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?