(本小题满分13分)已知直线 ,
, 相交于点
相交于点 .
.
(1)求点 的坐标;
的坐标;
(2)求以点 为圆心,且与直线
为圆心,且与直线 相切的圆的方程;
相切的圆的方程;
(3)若直线 与(2)中的圆
与(2)中的圆 交于
交于 、
、 两点,求
两点,求 面积的最大值及实数
面积的最大值及实数 的值.
的值.
(本小题满分14分)如图,在四面体 中,
中, ,点
,点 是
是 的中点,点
的中点,点 在线段
在线段 上,且
上,且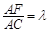 .
.
(1)若 ∥平面
∥平面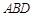 ,求实数
,求实数 的值;
的值;
(2)求证:平面 平面
平面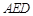 .
.
(本小题满分14分)
已知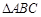 的三个内角
的三个内角 所对的边分别为
所对的边分别为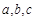 ,向量
,向量 ,
, ,且
,且 .
.
(1)求角A的大小;
(2)若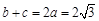 ,求证:
,求证: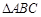 为等边三角形.
为等边三角形.
已知实数 ,函数
,函数 .
.
(1)当 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)若 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)若当 时,函数
时,函数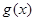 图象上的点均在不等式
图象上的点均在不等式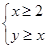 ,所表示的平面区域内,求实数
,所表示的平面区域内,求实数 的取值范围.
的取值范围.
(本小题16分)已知数列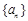 的各项均为正数,数列
的各项均为正数,数列 ,
, 满足
满足 ,
, .
.
(1)若数列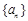 为等比数列,求证:数列
为等比数列,求证:数列 为等比数列;
为等比数列;
(2)若数列 为等比数列,且
为等比数列,且 ,求证:数列
,求证:数列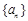 为等比数列.
为等比数列.
(本小题满分16分)如图,等腰梯形 的三边
的三边 分别与函数
分别与函数 ,
, 的图象切于点
的图象切于点 .求梯形
.求梯形 面积的最小值.
面积的最小值.