在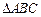
中, a，b，c分别是A、B、C的对边，且
.
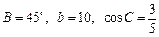(1)求a的值；
(2)设D为AB的中点，求中线CD的长.
已知椭圆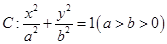
，过焦点垂直于长轴的弦长为1，且焦点与短轴两端点构成等边三角形.
（1）求椭圆的方程；
（2）过点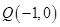
的直线l交椭圆于A，B两点，交直线
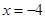于点E，
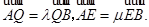判断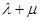
是否为定值，若是，计算出该定值；不是，说明理由.
设数列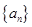
为等差数列，且
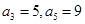；数列
的前n项和为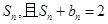
.
（1）求数列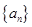，的通项公式；
（2）若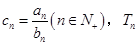
为数学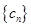
的前n项和，求
.
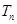如图，在多面体
中，四边形
是正方形，AC=AB=1，
.
（1）求证：
；
（2）求二面角
的余弦值的大小.
甲、乙两篮球运动员进行定点投篮，每人各投4个球，甲投篮命中的概率为
，乙投篮命中的概率为
.
（1）求甲至多命中2个且乙至少命中2个的概率；
（2）若规定每投篮一次命中得3分，未命中得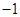
分，求乙所得分数
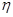的概率分布和数学期望.
已知向量
，函数
的最小正周期为
.
（1）求函数
的单调增区间；
（2）如果△ABC的三边
所对的角分别为
，且满足
的值.