已知椭圆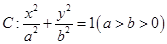
，过焦点垂直于长轴的弦长为1，且焦点与短轴两端点构成等边三角形.
（1）求椭圆的方程；
（2）过点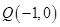
的直线l交椭圆于A，B两点，交直线
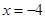于点E，
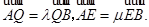判断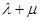
是否为定值，若是，计算出该定值；不是，说明理由.
（本小题满分13分）设函数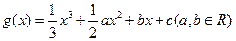
的图象经过原点，在其图象上一点P（x，y）处的切线的斜率记为
.
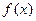（1）若方程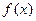=0有两个实根分别为-2和4,求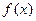的表达式；
（2）若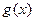
在区间[-1,3]上是单调递减函数,求
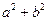的最小值.
定义在R上的单调函数f(x)满足f(3)=log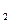
3且对任意x，y∈R都有f(x+y)=f(x)+f(y)．
(1)求证f(x)为奇函数；
(2)若f(k·3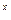
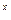)+f(3-9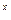-2)＜0对任意x∈R恒成立，求实数k的取值范围．
已知函数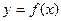
是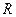
上的奇函数，当
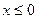时，
，
（1）判断并证明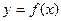在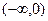
上的单调性；
（2）求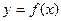的值域；
（3）求不等式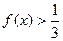
的解集。
已知函数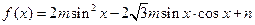
的定义域为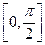
，值域为
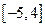．试求函数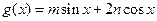
（
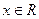）的最小正周期和最值
在锐角三角形ABC中，已知内角A、B、C所对的边分别为a、b、c，且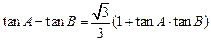
．
（1）若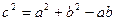
，求A、B、C的大小；
（2）已知向量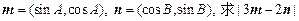
的取值范围．