(本小题满分13分)设函数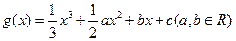 的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为
的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为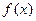 .
.
(1)若方程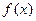 =0有两个实根分别为-2和4,求
=0有两个实根分别为-2和4,求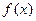 的表达式;
的表达式;
(2)若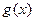 在区间[-1,3]上是单调递减函数,求
在区间[-1,3]上是单调递减函数,求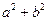 的最小值.
的最小值.
某单位 名员工参加“社区低碳你我他”活动.他们的年龄在
名员工参加“社区低碳你我他”活动.他们的年龄在 岁至
岁至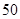 岁
岁
之间.按年龄分组:第1组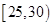 ,第
,第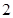 组
组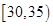 ,第3组
,第3组 ,第
,第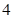 组
组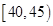 ,第
,第 组
组 ,得到的频率分布直方图如图所示.下表是年龄的频率分布表.
,得到的频率分布直方图如图所示.下表是年龄的频率分布表.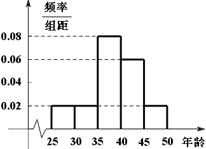
| 区间 |
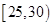 |
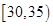 |
 |
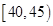 |
 |
| 人数 |
 |
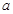 |
 |
(1)求正整数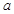 、
、 、
、 的值;
的值;
(2)现要从年龄较小的第 、
、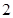 、
、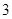 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取 人,则年龄在第
人,则年龄在第 、
、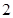 、
、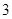 组的人数分别
组的人数分别
是多少?
(3)在(2)的条件下,从这 人中随机抽取
人中随机抽取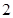 人参加社区宣传交流活动,求恰有
人参加社区宣传交流活动,求恰有 人在第
人在第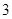 组的概率.
组的概率.
在△ 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且
,且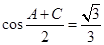 .
.
(1)求 的值;
的值;
(2)若 ,
, ,求
,求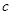 的值.
的值.
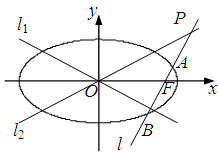
如图,已知椭圆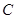 的方程为
的方程为 ,双曲线
,双曲线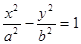 的两条渐近线为
的两条渐近线为 、
、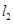 .过椭圆
.过椭圆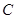 的右焦点
的右焦点 作直线
作直线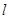 ,使
,使 ,又
,又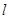 与
与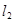 交于点
交于点 ,设
,设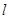 与椭圆
与椭圆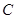 的两个交点由上至下依次为
的两个交点由上至下依次为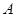 、
、 .
.
(1)若 与
与 的夹角为
的夹角为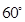 ,且双曲线的焦距为
,且双曲线的焦距为 ,求椭圆
,求椭圆 的方程;
的方程;
(2)求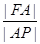 的最大值.
的最大值.
设函数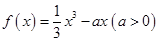 ,
,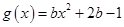 .
.
(1)若曲线 与
与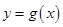 在它们的交点
在它们的交点 处有相同的切线,求实数
处有相同的切线,求实数 、
、 的值;
的值;
(2)当 时,若函数
时,若函数 在区间
在区间 内恰有两个零点,求实数
内恰有两个零点,求实数 的取值范围;
的取值范围;
(3)当 ,
, 时,求函数
时,求函数 在区间
在区间 上的最小值.
上的最小值.
已知数列{an}满足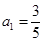 ,
,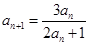 ,
,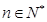 .
.
(1)求证:数列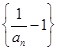 为等比数列;
为等比数列;
(2)是否存在互不相等的正整数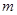 、
、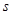 、
、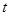 ,使
,使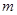 、
、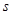 、
、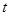 成等差数列,且
成等差数列,且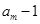 、
、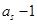 、
、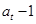 成等比数列?如果存在,求出所有符合条件的
成等比数列?如果存在,求出所有符合条件的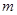 、
、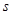 、
、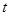 ;如果不存在,请说明理由.
;如果不存在,请说明理由.