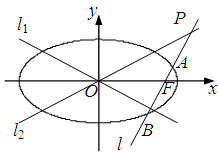
如图,已知椭圆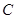 的方程为
的方程为 ,双曲线
,双曲线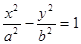 的两条渐近线为
的两条渐近线为 、
、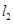 .过椭圆
.过椭圆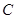 的右焦点
的右焦点 作直线
作直线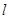 ,使
,使 ,又
,又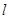 与
与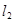 交于点
交于点 ,设
,设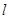 与椭圆
与椭圆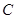 的两个交点由上至下依次为
的两个交点由上至下依次为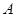 、
、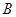 .
.
(1)若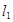 与
与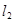 的夹角为
的夹角为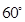 ,且双曲线的焦距为
,且双曲线的焦距为 ,求椭圆
,求椭圆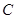 的方程;
的方程;
(2)求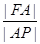 的最大值.
的最大值.
设函数 .
.
(1)对于任意实数 ,
, 恒成立,求
恒成立,求 的最大值;
的最大值;
(2)若方程 有且仅有一个实根,求
有且仅有一个实根,求 的取值范围.
的取值范围.
已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,且
,且 。
。
(1)求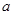 的值,(2)求
的值,(2)求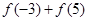 的值.
的值.
已知命题p:“ x∈[1,2],2x2-a≥0”,命题q:“
x∈[1,2],2x2-a≥0”,命题q:“ x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围。
x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围。
已知全集 R,
R, ,
, .
.
(1)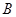

 ;
;
(2)若不等式 的解集为
的解集为 ,求
,求 、
、 的值
的值
设函数f(x)=lnx-ax+ -1.
-1.
(1) 当a=1时, 过原点的直线与函数f(x)的图象相切于点P, 求点P的坐标;
(2) 当0<a< 时, 求函数f(x)的单调区间;
时, 求函数f(x)的单调区间;
(3) 当a= 时, 设函数g(x)=x2-2bx-
时, 设函数g(x)=x2-2bx-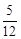 , 若对于
, 若对于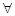 x1∈
x1∈ ,
, 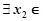 [0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<
[0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<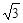 +1).
+1).