某单位 名员工参加“社区低碳你我他”活动.他们的年龄在
名员工参加“社区低碳你我他”活动.他们的年龄在 岁至
岁至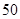 岁
岁
之间.按年龄分组:第1组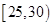 ,第
,第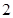 组
组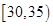 ,第3组
,第3组 ,第
,第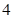 组
组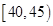 ,第
,第 组
组 ,得到的频率分布直方图如图所示.下表是年龄的频率分布表.
,得到的频率分布直方图如图所示.下表是年龄的频率分布表.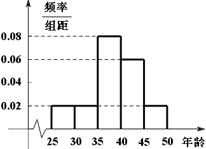
| 区间 |
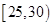 |
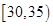 |
 |
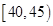 |
 |
| 人数 |
 |
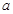 |
 |
|
|
(1)求正整数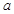 、
、 、
、 的值;
的值;
(2)现要从年龄较小的第 、
、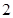 、
、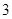 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取 人,则年龄在第
人,则年龄在第 、
、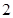 、
、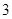 组的人数分别
组的人数分别
是多少?
(3)在(2)的条件下,从这 人中随机抽取
人中随机抽取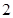 人参加社区宣传交流活动,求恰有
人参加社区宣传交流活动,求恰有 人在第
人在第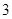 组的概率.
组的概率.
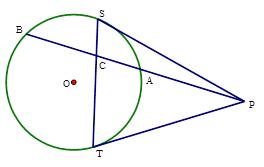
如图所示,已知点P是⊙O外一点,PS、PT是⊙O的两条切线,过点P作⊙O
的割线PAB,交⊙O于A、B两点,与ST交于点C,求证: 
已知x1、x2是关于x的一元二次方程x2+(3a-1)x+2a2-1=0的两个实数根,使得
(3x1-x2)(x1-3x2)=-80成立.求实数a的所有可能值.
在某服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元,并且每周(7天)涨价2元,从第6周开始保持30元的价格平稳销售;从第12周开始,当季节即将过去时,平均每周减价2元,直到第16周周末,该服装不再销售。
⑴试建立销售价y与周次x之间的函数关系式;
⑵若这种时装每件进价Z与周次 次之间的关系为Z=
次之间的关系为Z=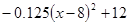 ,1≤
,1≤ ≤16,且
≤16,且 为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?
为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?
如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,
DG∥BC,求正方形DEFG面积的最大值.
已知过抛物线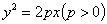 的焦点,斜率为
的焦点,斜率为 的直线交抛物线于
的直线交抛物线于
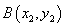 (
( )两点,且
)两点,且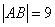 .
.
(1)求该抛物线的方程;
(2) 为坐标原点,
为坐标原点,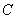 为抛物线上一点,若
为抛物线上一点,若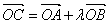 ,求
,求 的值.
的值.