定义在R上的单调函数f(x)满足f(3)=log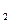 3且对任意x,y∈R都有f(x+y)=f(x)+f(y).
3且对任意x,y∈R都有f(x+y)=f(x)+f(y).
(1)求证f(x)为奇函数;
(2)若f(k·3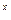 )+f(3
)+f(3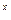 -9
-9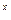 -2)<0对任意x∈R恒成立,求实数k的取值范围.
-2)<0对任意x∈R恒成立,求实数k的取值范围.
(本大题满分13分)如图,现有一块半径为2m,圆心角为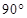 的扇形铁皮
的扇形铁皮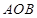 ,欲从其中裁剪出一块内接五边形
,欲从其中裁剪出一块内接五边形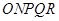 ,使点
,使点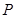 在
在 弧上,点
弧上,点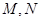 分别在半径
分别在半径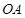 和
和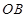 上,四边形
上,四边形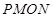 是矩形,点
是矩形,点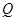 在弧
在弧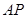 上,
上,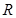 点在线段
点在线段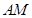 上,四边形
上,四边形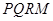 是直角梯形.现有如下裁剪方案:先使矩形
是直角梯形.现有如下裁剪方案:先使矩形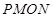 的面积达到最大,在此前提下,再使直角梯形
的面积达到最大,在此前提下,再使直角梯形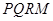 的面积也达到最大.
的面积也达到最大.
(Ⅰ)设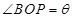 ,当矩形
,当矩形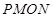 的面积最大时,求
的面积最大时,求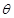 的值;
的值;
(Ⅱ)求按这种裁剪方法的原材料利用率.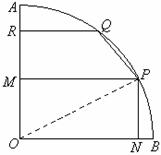
本大题满分13分)
已知函数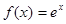 ,过该函数图象上点
,过该函数图象上点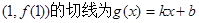
(Ⅰ)证明: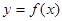 图象上的点总在
图象上的点总在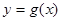 图象的上方;
图象的上方;
(Ⅱ)若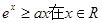 上恒成立,求实数
上恒成立,求实数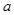 的取值范围.
的取值范围.
(本大题满分12分)设函数f(x)=x2+x-.
(1)若函数的定义域为[0,3],求f(x)的值域;
(2)若定义域为[a,a+1]时,f(x)的值域是[-,],求a的值.
(本大题满分12分)在△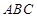 中,
中,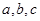 分别为内角
分别为内角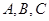 的对边,且
的对边,且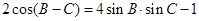
(1)求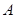
(2)若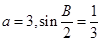 ,求
,求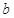
(本大题满分12分)已知点
(1)若 ,求
,求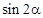 的值;
的值;
(2)若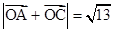 ,其中
,其中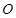 是原点,且
是原点,且 ,求
,求 与
与 的夹角。
的夹角。