甲、乙两篮球运动员进行定点投篮，每人各投4个球，甲投篮命中的概率为
，乙投篮命中的概率为
.
（1）求甲至多命中2个且乙至少命中2个的概率；
（2）若规定每投篮一次命中得3分，未命中得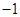
分，求乙所得分数
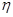的概率分布和数学期望.
已知函数
，曲线
在点x=1处的切线为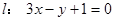
，若
时，有极值。
（1）求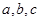
的值； （2）求在
上的最大值和最小值。
函数
的最小值为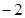
，其图象
相邻的最高点和最低点横坐标差是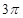
,又图象过点
.
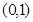(Ⅰ)求这个函数的解析式.；
(Ⅱ)画出函数在一个周期内的图象，并指出其单调减区间.
某商品在近30天内，每件的销售价格
（元）与时间
（天）的函
数关系是：
，该商品的日销售量Q(件)与时间t（天）
的函数关系是
，求这种商品日销售金额的最大值，
并指出日销售金额最大的一天是30天中的哪一天？
已知函数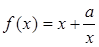
且
．
(Ⅰ)求
的值；
(Ⅱ)判断函数
在
上的单调性，并证明你的结论.
二次函数
的最小值为1，且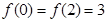
.
(Ⅰ)求的解析式；
(Ⅱ)若在区间
上不单调，求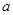
的取值范围．