如图，四边形ABCD为菱形，点E为对角线AC上的一个动点，连结DE并延长交AB于点F，连结BE．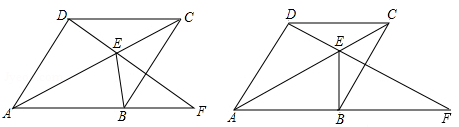
（1）如图①，求证：∠AFD=∠EBC；
（2）如图②，若DE=EC且BE⊥AF，求∠DAB的度数；
（3）若∠DAB=90°且当△BEF为等腰三角形时，求∠EFB的度数（只写出条件与对应的结果）
基本事实：若
（a>0且a≠1，m、n是正整数），则m＝n．
试利用上述基本事实分别求下列各等式中x的值：
①
；②
．
（本题6分）AB⊥BC，∠1+∠2=90°，∠2=∠3．BE与DF平行吗？为什么？
解：BE∥DF．
∵AB⊥BC，
∴∠ABC=°，
即∠3+∠4=°．
又∵∠1+∠2=90°，
且∠2=∠3，
∴=．
理由是：________________．
∴BE∥DF．
理由是：________________．
（本题6分）如图，在△ABC中，∠BAC是钝角，请画出AB边上的高CD，BC边上的中线AE，并将△ABC沿AE方向平移AE的长度．（请保留作图痕迹，）
化简求值：已知
，求代数式
的值．
（1）
（2）
（3）
（4）