如图1,在平面直角坐标系中,第一象限内长方形ABCD , AB∥y轴,点A(1,1),点C(a, b), 满足 .
.
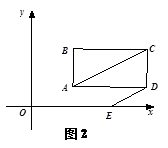
(1)求长方形ABCD的面积.
(2)如图2,长方形ABCD以每秒1个单位长度的速度向右平移,同时点E从原点O出发沿x轴以每秒2 个单位长度的速度向右运动,设运动时间为t秒.
①当t=4时,直接写出三角形OAC的面积为_______.
② 若AC∥ED,求t 的值;
(3)在平面直角坐标系中,对于点 ,我们把点
,我们把点 叫做点
叫做点 的伴随点,已知点
的伴随点,已知点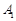 的伴随点为
的伴随点为 ,点
,点 的伴随点为
的伴随点为 ,点
,点 的伴随点为
的伴随点为 ,…,这样依次得到点
,…,这样依次得到点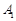 ,
, ,
, ,…,
,…, .
.
①若点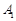 的坐标为(3,1),则点
的坐标为(3,1),则点 的坐标为 ,点
的坐标为 ,点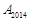 的坐标为 ;
的坐标为 ;
②若点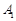 的坐标为(
的坐标为(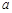 ,
, ),对于任意的正整数
),对于任意的正整数 ,点
,点 均在
均在 轴上方,则
轴上方,则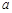 ,
, 应满足的条件为 .
应满足的条件为 .
已知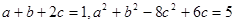 ,求
,求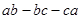 的值。
的值。
根据如图所示的(1),(2),(3)三个图所表示的规律,依次下去第n个图中平行四边形的个数是___________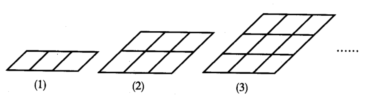
如图,已知AB//CD,试问:∠1、∠2、∠3有什么关系?请证明你的结论。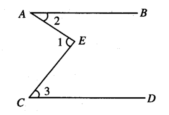
某服装专卖店老板对第一季度男、女服装的销售收入进行统计,并绘制了扇形统计图(如图)。由于三月份开展促销活动,男、女服装的销售收入分别比二月份增长了40%和64%,已知第一季度男女服装的销售总收入为20万元。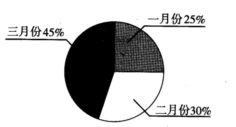
(1)一月份销售收入为_____________万元,
二月份销售收入为___________万元,
三月份销售收入为___________万元,
(2)列方程(组)求二月份男、女服装的销售收入分别是多少万元?
填空题:如图,AB//CD,∠ABC=50°,∠CPN=150°,∠PNB=60°,∠NDC=60°,求∠BCP的度数。
解: ,(已知)
,(已知)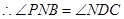 ,(等量代换)
,(等量代换) ___________//__________,()
___________//__________,() _________=180°,()
_________=180°,()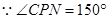 ,(已知)
,(已知)
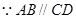 ,(已知)
,(已知)
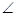 ____________,()
____________,() ,(已知)
,(已知) __________,(等量代换)
__________,(等量代换)
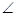 BCP=
BCP=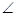 BCD-
BCD-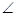 PCD=____________°-________°=_________°
PCD=____________°-________°=_________°