请将下列证明过程补充完整:
已知:如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N, .
.
求证: .
.
证明:因为 (已知),
(已知),
又因为 ( ),
( ),
所以 (等量代换).
所以 ∥ (同位角相等,两直线平行),
所以 ( ).
( ).
又因为 (已知),
(已知),
所以 ∥ ( ).
所以 (两直线平行,内错角相等).
所以 ( ).
( ).
已知△ABC,AB=AC,将△ABC沿BC方向平移得到△DEF.
(1)如图1,连接BD,AF,则BD AF(填“>”、“<”或“=”);
(2)如图2,M为AB边上一点,过M作BC的平行线MN分别交边AC,DE,DF于点G,H,N,连接BH,GF,求证:BH=GF.
如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据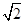 ≈1.4,
≈1.4,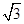 ≈1.7)
≈1.7)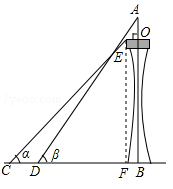
如图,一条输电线路从A地到B地需要经过C地,图中AC=20千米,∠CAB=30°,∠CBA=45°,因线路整改需要,将从A地到B地之间铺设一条笔直的输电线路.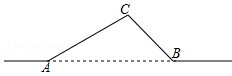
(1)求新铺设的输电线路AB的长度;(结果保留根号)
(2)问整改后从A地到B地的输电线路比原来缩短了多少千米?(结果保留根号)
补充完整三角形中位线定理,并加以(1)三角形中位线定理:三角形的中位线 ;
(2)已知:如图,DE是△ABC的中位线,求证:DE∥BC,DE=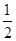 BC.
BC.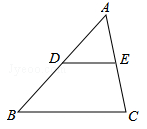
(为方便答题,可在答题卡上画出你认为必要的图形)
在Rt△ABC中,∠A=90°,AC =" AB" = 4,D,E分别是边AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰RtRt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)如图1,当α=90°时,线段BD1的长等于 ,线段CE1的长等于 ;(直接填写结果)
(2)如图2,当α=135°时,求证:BD1 = CE1 ,且BD1⊥ CE1 ;
(3)求点P到AB所在直线的距离的最大值.(直接写出结果)