如图,在△ABC中,MN∥BD交AC于点P, 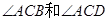 的平分线分别交MN于点E,F。
的平分线分别交MN于点E,F。
(1)求证:PE=PF
(2)当MN与AC的交点P在什么位置时,四边形AECF是矩形,请说明理由;
(3)当△ABC满足什么条件时,四边形AECF是正方形(不需证明)
如图,直线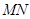 与线段
与线段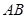 相交于点
相交于点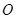 ,点
,点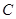 和点
和点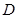 在直线
在直线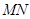 上,且
上,且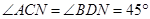 .
.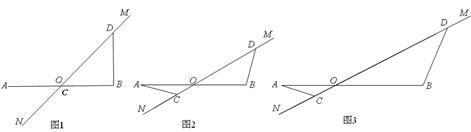
(1)如图1所示,当点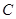 与点
与点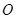 重合时 ,且
重合时 ,且 ,请写出
,请写出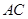 与
与 的数量关系和位置关系;
的数量关系和位置关系;
(2)将图1中的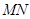 绕点
绕点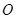 顺时针旋转到如图2所示的位置,
顺时针旋转到如图2所示的位置,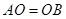 ,(1)中的
,(1)中的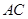 与
与 的数量关系和位置关系是否仍然成立?若成立,请证明;若不成立,请说明理由;
的数量关系和位置关系是否仍然成立?若成立,请证明;若不成立,请说明理由;
(3)将图2中的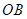 拉长为
拉长为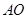 的
的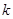 倍得到如图3,求
倍得到如图3,求 的值.
的值.
已知抛物线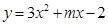 .
. 
(1)求证:无论 为任何实数,抛物线与x轴总有两个交点;
为任何实数,抛物线与x轴总有两个交点;
(2)若 为整数,当关于x的方程
为整数,当关于x的方程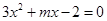 的两个有理数根都在
的两个有理数根都在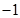 与
与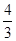 之间(不包括-1、
之间(不包括-1、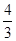 )时,求
)时,求 的值.
的值.
(3)在(2)的条件下,将抛物线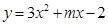 在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新图象
在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新图象 ,再将图象
,再将图象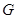 向上平移
向上平移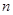 个单位,若图象
个单位,若图象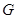 与过点(0,3)且与x轴平行的直线有4个交点,直接写出n的取值范围是.
与过点(0,3)且与x轴平行的直线有4个交点,直接写出n的取值范围是.
问题:如果存在一组平行线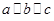 ,请你猜想是否可以作等边三角形
,请你猜想是否可以作等边三角形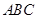 使其三个顶点分别在
使其三个顶点分别在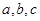 上.
上.
小明同学的解答如下:如图1所示,过点 作
作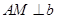 于
于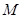 ,作
,作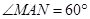 ,且
,且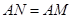 ,过点
,过点 作
作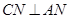 交直线
交直线 于点
于点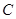 ,在直线
,在直线 上取点
上取点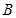 使
使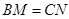 ,则
,则 为所求.
为所求.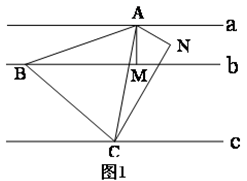
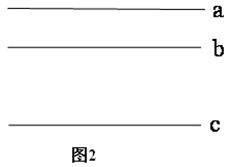
(1)请你参考小明的作法,在图2中作一个等腰直角三角形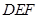 使其三个顶点分别在
使其三个顶点分别在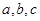 上,点
上,点 为直角顶点;
为直角顶点;
(2)若直线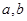 之间的距离为1,
之间的距离为1,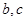 之间的距离为2,则在图2中,
之间的距离为2,则在图2中,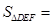 ,在图1中,
,在图1中,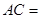 .
.
甲、乙两学校都选派相同人数的学生参加综合素质测试,测试结束后,发现每名参赛学生的成绩都是70分、80分、90分、100分这四种成绩中的一种,并且甲、乙两学校的学生获得100分的人数也相等.根据甲学校学生成绩的条形统计图和乙学校学生成绩的扇形统计图,解答下列问题: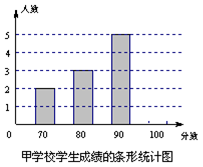
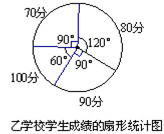
(1)求甲学校学生获得100分的人数,并补全统计图;
(2)分别求出甲、乙两学校学生这次综合素质测试所得分数的中位数和平均数,以此比较哪个学校的学生这次测试的成绩更好些.
已知:如图, 是Rt
是Rt ABC的外接圆,
ABC的外接圆, ABC=90
ABC=90 ,点P是
,点P是 外一点,PA切
外一点,PA切 于点A,且PA=PB.
于点A,且PA=PB.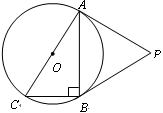
(1)求证:PB是 的切线;
的切线;
(2)已知PA= ,BC=2,求
,BC=2,求 的半径.
的半径.