重庆市移动公司2011年底手机用户量为100万部,预计2013年底手机用户量将达到144万部 .
(1)求2011年底至2013年底该公司手机用户量的年平均增长率;
(2)由于该公司的手机不断创新和开拓市场,预计到2015年底手机用户量将达到207.96万部.根据市场调查,从2013年底开始,手机用户每年减少的数量是上年底总数的5%.问从2014年初起,该公司每年新增手机的用户量是多少万部?(假定每年新增手机用户的数量相同)
先化简,再求值: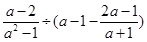 ,其中
,其中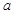 是方程
是方程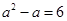 的根.
的根.
如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点均在格点上,在建立平面直角坐标系后,点C的坐标为(4,-1).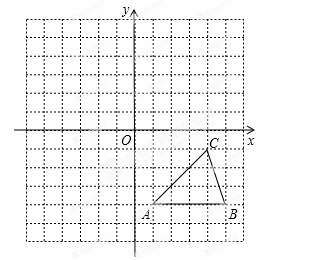
(1)画出△ABC以y轴为对称轴的对称图形△A1B1C1,并写出点C1的坐标;
(2)以原点O为对称中心,画出△A1B1C1关于原点O对称的△A2B2C2,并写出点C2的坐标;
(3)以A2为旋转中心,把△A2B2C2顺时针旋转90°,得到△A2B3C3,并写出点C3的坐标.
解方程 (1)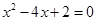 (2)
(2)
将两块大小相同的含30°角的直角三角板(∠BAC=∠B1A1C=30°)按图①的方式放置,固定三角板A1B1C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A1C交于点E,AC与A1B1交于点F,AB与A1B1交于点O.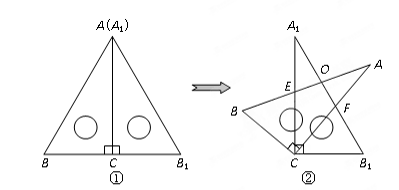
(1)求证:△BCE≌△B1CF.
(2)当旋转角等于30°时,AB与A1B1垂直吗?请说明理由.