如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是 ;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD= AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
(1)计算: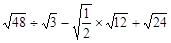
(2)先化简,再求值: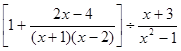 ,其中
,其中 。
。
如图,A,B,C,D,E,F,M,N是某公园里的8个独立的景点,D,E,B三个景点之间的距离相等;A,B,C三个景点距离相等.其中D,B,C在一条直线上,E,F,N,C在同一直线上,D,M,F,A也在同一条直线上.游客甲从E点出发,沿E→F→N→C→A→B→M游览,同时,游客乙从D点出发,沿D→M→F→A→C→B→N游览.若两人的速度相同且在各景点游览的时间相同,甲、乙两人谁最先游览完?请说明理由.
如图,矩形ABCD中,AB=4,BC=9,动点Q沿着C→D→A→B的方向运动至点B停止,设点Q运动的路程为x,△QCB的面积为y.
(1)当点Q在CD上运动时,求y与x的关系式;
(2)当点Q在AD上运动时,△QCB的面积改变了吗?请说明理由.
(3)说一说y是怎样随着x的变化而变化的?
如图所示,图象反映的是:张阳从家里跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示张阳离家的距离.根据图象回答下列问题:
(1)体育场离张阳家_________千米;
(2)体育场离文具店_________千米;张阳在文具店逗留了_____分钟;
(3)请计算:张阳从文具店到家的平均速度约是每小时多少千米?
很多代数原理都可以用几何模型解释.现有若干张如图所示的卡片,请拼成一个边长为(2a+b)的正方形(要求画出简单的示意图),并指出每种卡片分别用了多少张?然后用相应的公式进行验证.