如图,抛物线y=ax2+bx(a≠0)经过点A(2,0),点B(3,3),BC⊥x轴于点C,连接OB,等腰直角三角形DEF的斜边EF在x轴上,点E的坐标为(﹣4,0),点F与原点重合
(1)求抛物线的解析式并直接写出它的对称轴;
(2)△DEF以每秒1个单位长度的速度沿x轴正方向移动,运动时间为t秒,当点D落在BC边上时停止运动,设△DEF与△OBC的重叠部分的面积为S,求出S关于t的函数关系式;
(3)点P是抛物线对称轴上一点,当△ABP时直角三角形时,请直接写出所有符合条件的点P坐标.
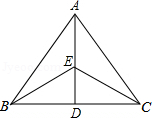
如图,在△ABC中,AB=AC,AD是角平分线,点E在AD上,请写出图中两对全等三角形,并选择其中的一对加以证明.
解方程: .
如图1,在△ ABC中,∠ ACB=90°,∠ B=30°, AC=4, D是 AB的中点, EF是△ ACD的中位线,矩形 EFGH的顶点都在△ ACD的边上.
(1)求线段 EF、 FG的长;
(2)如图2,将矩形 EFGH沿 AB向右平移,点 F落在 BC上时停止移动,设矩形移动的距离为 x,矩形与△ CBD重叠部分的面积为 S,求出 S关于 x的函数解析式;
(3)如图3,矩形 EFGH平移停止后,再绕点 G按顺时针方向旋转,当点 H落在 CD边上时停止旋转,此时矩形记作 E 1 F 1 GH 1,设旋转角为α,求cosα的值.

某车行经销的 A型自行车去年6月份销售总额为1.6万元,今年由于改造升级每辆车售价比去年增加200元,今年6月份与去年同期相比,销售数量相同,销售总额增加25%.
(1)求今年 A型车每辆售价多少元?
(2)该车行计划7月份用不超过4.3万元的资金新进一批 A型车和 B型车共50辆,应如何进货才能使这批车售完后获利最多?
今年 A, B两种型号车的进价和售价如下表:
|
A型车 |
B型车 |
|
|
进价(元/辆) |
800 |
950 |
|
售价(元/辆) |
今年售价 |
1200 |
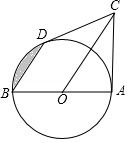
如图, AB是⊙ O的直径, CD切⊙ O于点 D,且 BD∥ OC,连接 AC.
(1)求证: AC是⊙ O的切线;
(2)若 AB= OC=4,求图中阴影部分的面积(结果保留根号和π)