(本小题满分10分)已知函数 的最小正周期为
的最小正周期为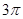 ,
,
(1)求函数 的表达式并求
的表达式并求 在区间
在区间 上的最小值;
上的最小值;
(2)在 中,
中, 分别为角
分别为角 所对的边,且
所对的边,且 ,
, ,求角
,求角 的大小;
的大小;
设函数 (a、b、c、d∈R)满足:对于任意的
(a、b、c、d∈R)满足:对于任意的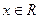 都有f(x)+f(-x)=0,且x=1时f(x)取极小值
都有f(x)+f(-x)=0,且x=1时f(x)取极小值 .
.
(1)f(x)的解析式;
(2)当 时,证明:函数图象上
时,证明:函数图象上 任意两点处的切线不可能互相垂直:
任意两点处的切线不可能互相垂直:
(本小题12分)
已知如下等式: ,
,
 ,
, ,当
,当 时,试猜想
时,试猜想 的值,并用数学归纳法给予证明。
的值,并用数学归纳法给予证明。
(本小题12分)
设复数 满足
满足 ,且
,且 是纯虚数,求复数
是纯虚数,求复数 的共轭复数
的共轭复数 。
。
(本小题满分12分)
通过计算可得下列等式: ,
, ,
, ,┅┅,
,┅┅,
将以上各式分别相加得:
即:
类比上述求法:请你求出 的值(要求必须有运算推理过程).
的值(要求必须有运算推理过程).
(本小题满分12分)
某研究机构为了研究人的体重与身高之间的关系,随机抽测了20人,得到如下 数据:
数据:
(1)若“身高大于175厘米”的为 “高个”,“身高小于等于175厘米”的为“非高个”;“体重大于75(公斤)”的为“胖子”,“体重小于等于75(公
“高个”,“身高小于等于175厘米”的为“非高个”;“体重大于75(公斤)”的为“胖子”,“体重小于等于75(公 斤)”的为“非胖子”.请根据上表数据完成下面的
斤)”的为“非胖子”.请根据上表数据完成下面的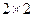 联列表:
联列表:
| 高个 |
非高个 |
合计 |
|
| 胖 子 |
|||
| 非胖子 |
12 |
||
| 合计 |
20 |
(2)根据题(1)中表格的数据,若按99%的可靠性要求,能否认为体重与身高之间有关系?