【问题提出】如图1，四边形ABCD中，AD=CD，∠ABC=120°，∠ADC=60°，AB=2，BC=1，求四边形ABCD的面积．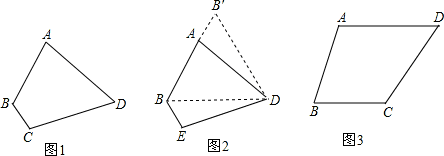

【尝试解决】
旋转是一种重要的图形变换，当图形中有一组邻边相等时，往往可以通过旋转解决问题．
（1）如图2，连接 BD，由于AD=CD，所以可将△DCB绕点D顺时针方向旋转60°，得到△DAB′，则△BDB′的形状是              ．
（2）在（1）的基础上，求四边形ABCD的面积．
[类比应用]如图3，四边形ABCD中，AD=CD，∠ABC=75°，∠ADC=60°，AB=2，BC=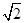，求四边形ABCD的面积．

科目 数学   题型 解答题   难度 较难

知识点： 对称式和轮换对称式