如图所示为半径R=0.50m的四分之一圆弧轨道,底端距水平地面的高度h=0.45m.一质量m=1.0kg的小滑块从圆弧轨道顶端A由静止释放,到达轨道底端B点的速度v=2.0m/s.忽略空气的阻力.取g=10m/s2.求:
(1)小滑块在圆弧轨道底端B点受到的支持力大小FN;
(2)小滑块由A到B的过程中,克服摩擦力所做的功W;
(3)小滑块落地点与B点的水平距离x.
一辆做匀加速直线运动的轿车,以5m/s2的加速度经过路边相距16m的两路标,它经过第一路标时的速度为3m/s,那么经过第二路标时的速度为多少 ?
如右图所示的电路中,两平行金属板A、B水平放置,两板间的距离d="40" cm.电源电动势E=24V,内电阻r=1Ω,电阻R=15Ω。闭合开关S,待电路稳定后,将一带正电的小球从B板小孔以初速度v0="4" m/s竖直向上射入板间。若小球带电荷量为q=1×10-2 C,质量为m=2×10-2 kg,不考虑空气阻力。那么,滑动变阻器接入电路的阻值为多大时,小球恰能到达A板?此时电源的输出功率是多大?(取g="10" m/s2)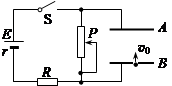
如图所示为两组平行金属板,一组竖直放置,一组水平放置,今有一质量为m的电子静止在竖直放置的平行金属板的A点,经电压U0加速后通过B点进入两板间距为d、电压为U的水平放置的平行金属板间,若电子从两块水平平行板的正中间射入,且最后电子刚好能从右侧的两块平行金属板穿出,A、B分别为两块竖直板的中点,求: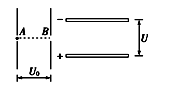
(1)电子通过B点时的速度大小;
(2)右侧平行金属板的长度;
(3)电子穿出右侧平行金属板时的动能.
已知电流表的内阻Rg=120 Ω,满偏电流Ig=3 mA,要把它改装成量程是6 V的电压表,应串联多大的电阻?要把它改装成量程是3 A的电流表,应并联多大的电阻?
带电量为Q,质量为m的原子核由静止开始经电压为U1的电场加速后进入一个平行板电容器,进入时速度和电容器中的场强方向垂直。已知:电容器的极板长为L,极板间距为d,两极板的电压为U2,重力不计,求:(1)经过加速电场后的速度;(2)离开电容器电场时的偏转量。