如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=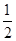 ,OB=4,OE=2.
,OB=4,OE=2.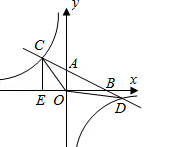
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
如图,直线CD与直线AB相交于C,根据下列语句画图、解答。过点P作PQ∥CD,交AB于点Q
过点P作PR⊥CD,垂足为R
若∠DCB=1200,猜想∠PQC是多少度?并说明理由
如图,A点在B处的北偏东40°方向,C点在B处的北偏东85°方向,
A点在C处的北偏西45°方向,求∠BAC及∠BCA的度数?
在平面直角坐标系中,顺次连结A(-2,0)、B(4,0)、C(-2,-3)各点,试求:A、B两点之间的距离。
点C到X轴的距离。
△ABC的面积。

如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D。
试说明:AC∥DF。
解:因为∠1=∠2(已知)
∠1=∠3,∠2=∠4()
所以∠3=∠4(等量代换)
所以∥()
所以∠C=∠ABD,()
又因为∠C=∠D(已知)
所以∠D=∠ABD(等量代换)
所以 AC∥DF()
如图,已知直线 被直线
被直线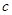 所截,
所截, ∥
∥ ,如果
,如果 ,求∠1的度数。
,求∠1的度数。