如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D。
试说明:AC∥DF。
解:因为∠1=∠2(已知)
∠1=∠3,∠2=∠4( )
所以∠3=∠4(等量代换)
所以 ∥ ( )
所以∠C=∠ABD,( )
又因为∠C=∠D(已知)
所以∠D=∠ABD(等量代换)
所以 AC∥DF( )
如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A′B′O.
(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;
(2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O面积4倍?若存在,请求出P的坐标;若不存在,请说明理由.
(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B的两条性质.
2013年我国多地出现雾霾天气,某企业抓住商机准备生产空气净化设备,该企业决定从以下两个投资方案中选择一个进行投资生产,方案一:生产甲产品,每件产品成本为a元(a为常数,且40<a<100),每件产品销售价为120元,每年最多可生产125万件;方案二:生产乙产品,每件产品成本价为80元,每件产品销售价为180元,每年可生产120万件,另外,年销售x万件乙产品时需上交0.5x2万元的特别关税,在不考虑其它因素的情况下:
(1)分别写出该企业两个投资方案的年利润y1(万元)、y2(万元)与相应生产件数x(万件)(x为正整数)之间的函数关系式,并指出自变量的取值范围;
(2)分别求出这两个投资方案的最大年利润;
(3)如果你是企业决策者,为了获得最大收益,你会选择哪个投资方案?
如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF.
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
日照市改善空气质量,开展“绿色家园”活动,加快了绿化荒山的速度,2013年市政府共投资4亿元人民币绿化荒山160万平方米,预计到2015年这三年共累计投资19亿元人民币绿化荒山.若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的绿化成本不变,预计2015年能绿化多少万平方米荒山?
2015年莒县中学生运动会刚刚闭幕.下面是某初中学校末制作完的三个年级县运动会志愿者的统计图.请你根据图中所给信息解答下列问题: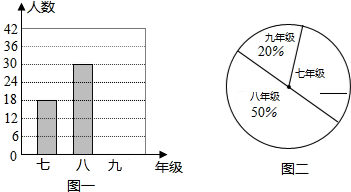
(1)请你求出九年级有多少名县运动会志愿者,并将两幅统计图补充完整;
(2)要求从七年级、九年级志愿者中推荐一名队长候选人,八年级志愿者中推荐两名队长候选人,四名候选人中选出两人任队长,用列表法或树形图,求出两名队长都是八年级志愿者的概率是多少?