如图,某建筑物BC上有一旗杆AB,小刘在与BC相距24m的F处,由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°,小刘的观测点与地面的距离EF为1.6m.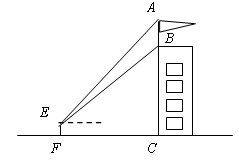
(1)求建筑物BC的高度;
(2)求旗杆AB的高度.
(结果精确到0.1m.参考数据: ≈1.41,sin52°≈0.79,tan52°≈1.28)
≈1.41,sin52°≈0.79,tan52°≈1.28)
先化简,再求值: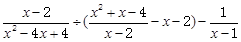 ,其中x是不等式组
,其中x是不等式组 的整数解。
的整数解。
目前我区“校园手机”现象越来越受到社会关注,针对这种现象,我区某中学九年级(1)班数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度(态度分为:A无所谓,B 基本赞成,C 赞成,D 反对),并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)根据抽样调查结果,请你估计我校11000名中学生家长中有多少名家长持反对态度;
(4)在此次调查活动中,九年级(1)班和初九年级(2)班各有2位家长对中学生带手机持反对态度,现从中选2位家长参加学校组织的家校活动,用列表法或画树 状图的方法求选出的2人来自不同班级的概率.
已知:∠B=∠C,AD=AE,∠1=∠2. 求证:BD=CE.
(本小题满分12分)如图, 在直角坐标系xOy中,一次函数y=- x+m(m为常数)的图像与x轴交于A(-3,0),与y轴交于点C。以直线x=-1为对称轴的抛物线y=a
x+m(m为常数)的图像与x轴交于A(-3,0),与y轴交于点C。以直线x=-1为对称轴的抛物线y=a +bx+c(a,b,c为常数,且a>0)经过A,C两点,与x轴正半轴交于点B.
+bx+c(a,b,c为常数,且a>0)经过A,C两点,与x轴正半轴交于点B.
(1)求一次函数及抛物线的函数表达式。
(2)已知在对称轴上是否存在一点P,使得 PBC的周长最小,若存在,请求出点P的坐标.
PBC的周长最小,若存在,请求出点P的坐标.
(3)点D是线段OC上的一个动点(不与点O、点C重合),过点D作DE‖PC交x轴于点E,连接PD、PE。设CD的长为m, △PDE的面积为S。求S与m之间的函数关系式。并说明S是否存在最大值,若存在,请求出最大值:若不存在,请说明理由。