某校为了解2014年八年级学生课外书籍借阅情况,从中随机抽取了50名学生课外书籍借阅情况,将统计结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这50名学生借阅总册数的40%.
| 类别 |
科普类 |
教辅类 |
文艺类 |
其他 |
| 册数(本) |
168 |
105 |
m |
32 |
(1)表格中字母m的值等于 ;
(2)扇形统计图中“教辅类”所对应的圆心角α的度数为 °;
(3)该校2014年八年级有600名学生,请你估计该年级学生共借阅教辅类书籍约多少本?
如图,四边形ABCD是矩形,用直尺和圆规作出∠A的平分线与BC边的垂直平分线的交点Q(不写作法,保留作图痕迹).连结QD,在新图形中,你发现了什么?请写出一条.
如图,三角形ABC是以BC为底边的等腰三角形,点A、C分别是一次函数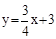 的图象与y轴的交点,点B在二次函数
的图象与y轴的交点,点B在二次函数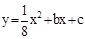 的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.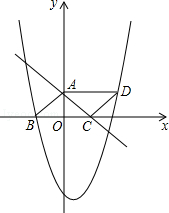
(1)试求b,c的值,并写出该二次函数表达式;
(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:
①当P运动到何处时,有PQ⊥AC?
②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?
已知:关于x的一元二次方程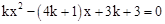 (k是整数).
(k是整数).
(1)求证:方程有两个不相等的实数根;
(2)若方程的两个实数根分别为x1,x2(其中x1<x2),设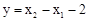 ,判断y是否为变量k的函数?如果是,请写出函数解析式;若不是,请说明理由.
,判断y是否为变量k的函数?如果是,请写出函数解析式;若不是,请说明理由.
某小区为了促进生活垃圾的分类处理,将生活垃圾分为厨余、可回收和其他三类,分别记为a,b,c,并且设置了相应的垃圾箱,“厨余垃圾”箱、“可回收物”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若将三类垃圾随机投入三类垃圾箱,请用画树状图的方法求垃圾投放正确的概率;
(2)为调查居民生活垃圾分类投放情况,现随机抽取了该小区三类垃圾箱中总共1 000吨生活垃圾,数据统计如下(单位:吨):
试估计“厨余垃圾”投放正确的概率.
如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.
(1)求证:AP是⊙O的切线;
(2)OC=CP,AB=6,求CD的长.