若关于 的不等式
的不等式 在区间
在区间 上有解,则实数
上有解,则实数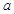 的取值范围为( )
的取值范围为( )
A. |
B. |
C.(1,+∞) | D.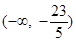 |
已知 是两个非零向量,给定命题
是两个非零向量,给定命题 ,命题
,命题 ,使得
,使得 ,则
,则 是
是 的()
的()
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知集合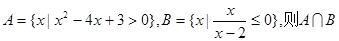 等于()
等于()
A. |
B.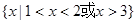 |
C. |
D.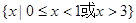 |
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”,已知函数
的“隔离直线”,已知函数 ,有下列命题:
,有下列命题:
① 在
在 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且 的最小值为
的最小值为 ;
;
③ 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且 的取值范围是
的取值范围是 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有()
A. 个 个 |
B. 个 个 |
C. 个 个 |
D. 个 个 |
已知定义域为 的奇函数
的奇函数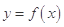 的导函数为
的导函数为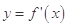 ,当
,当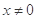 时
时 ,若
,若 ,
,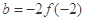 ,
,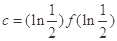 ,则
,则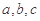 的大小关系是()
的大小关系是()
A. |
B.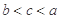 |
C. |
D.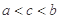 |
已知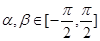 ,
, ,则下列不等式一定成立的是()
,则下列不等式一定成立的是()
A.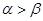 |
B.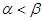 |
C.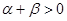 |
D.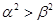 |