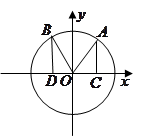
(本小题满分12分)如图,在平面直角坐标系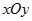 中,点
中,点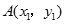 在单位圆
在单位圆 上,
上, ,且
,且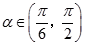 .
.
(1)若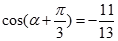 ,求
,求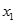 的值;
的值;
(2)若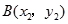 也是单位圆
也是单位圆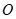 上的点,且
上的点,且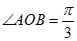 .过点
.过点 分别做
分别做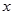 轴的垂线,垂足为
轴的垂线,垂足为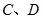 ,记
,记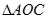 的面积为
的面积为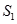 ,
, 的面积为
的面积为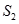 .设
.设 ,求函数
,求函数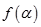 的最大值.
的最大值.
设数列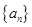 的各项均为正数.若对任意的
的各项均为正数.若对任意的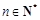 ,存在
,存在 ,使得
,使得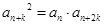 成立,则称数列
成立,则称数列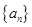 为“Jk型”数列.
为“Jk型”数列.
(1)若数列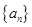 是“J2型”数列,且
是“J2型”数列,且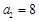 ,
, ,求
,求 ;
;
(2)若数列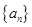 既是“J3型”数列,又是“J4型”数列,证明:数列
既是“J3型”数列,又是“J4型”数列,证明:数列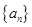 是等比数列.
是等比数列.
如图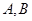 是单位圆
是单位圆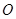 上的点,
上的点, 分别是圆
分别是圆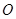 与
与 轴的两交点,
轴的两交点,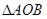 为正三角形.
为正三角形.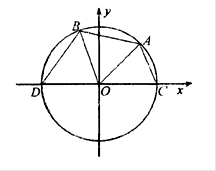
(1)若 点坐标为
点坐标为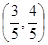 ,求
,求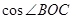 的值;
的值;
(2)若 ,四边形
,四边形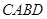 的周长为
的周长为 ,试将
,试将 表示成
表示成 的函数,并求出
的函数,并求出 的最大值.
的最大值.
已知在等比数列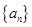 中,
中,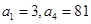 ,若数列
,若数列 满足:
满足: ,数列
,数列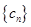 满足:
满足: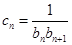 ,且数列
,且数列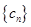 的前
的前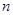 项和为
项和为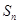 .
.
(1)求数列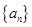 的通项公式;(2)求数列
的通项公式;(2)求数列 的通项公式; (3) 求
的通项公式; (3) 求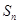 .
.
在△ 中,∠
中,∠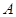 ,∠
,∠ ,∠
,∠ 的对边分别是
的对边分别是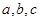 ,且
,且  .
.
(1)求∠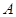 的大小;(2)若
的大小;(2)若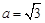 ,
, ,求
,求 和
和 的值.
的值.
已知函数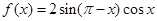 .
.
(1)求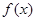 的最小正周期; (2)求
的最小正周期; (2)求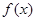 在区间
在区间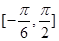 上的最大值和最小值.
上的最大值和最小值.