如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．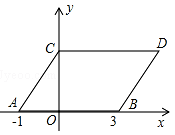
（1）求点C，D的坐标；
（2）若在y轴上存在点 M，连接MA，MB，使S△MAB=S平行四边形ABDC，求出点M的坐标．
（3）若点P在直线BD上运动，连接PC，PO．
①若P在线段BD之间时（不与B，D重合），求S△CDP+S△BOP的取值范围；
②若P在直线BD上运动，请直接写出∠CPO、∠DCP、∠BOP的数量关系．
如图，在△ABC中，AB=AC，点D、E、F分别在AB、BC、AC边上，且BE=CF，BD=CE．
（1）求证：DE=EF；
（2）当∠A=50°时，求∠DEF的度数；
已知5a-1的平方根是
，6a+2b-1的立方根是3，求b-4a的平方根．
求满足下列等式中的x的值：
（1）
（2）
用四块长为acm、宽为bcm的矩形材料（如图1）拼成一个大矩形（如图2）或大正方形（如图3），中间分别空出一个小矩形A和一个小正方形B．
（1）求（如图1）矩形材料的面积；（用含a，b的代数式表示）
（2）通过计算说明A、B的面积哪一个比较大；
（3）根据（如图4），利用面积的不同表示方法写出一个代数恒等式．
如图，某市有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像，则绿化的面积是多少平方米？并求出当a=3，b=2时的绿化面积．