如图,已知直线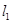 ∥
∥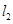 ,
,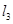 、
、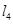 和
和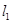 、
、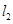 分别交于点
分别交于点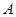 、
、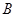 、
、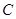 、
、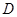 ,点
,点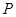 在直线
在直线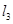 或
或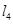 上且不与点
上且不与点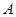 、
、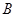 、
、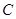 、
、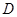 重合.记
重合.记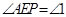 ,
,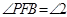 ,
,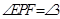 .
.
(1)若点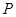 在图(1)位置时,求证:
在图(1)位置时,求证: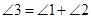 ;
;
(2)若点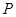 在图(2)位置时,请直接写出
在图(2)位置时,请直接写出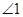 、
、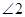 、
、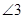 之间的关系;
之间的关系;
(3)若点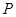 在图(3)位置时,写出
在图(3)位置时,写出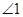 、
、 、
、 之间的关系并给予证明.
之间的关系并给予证明.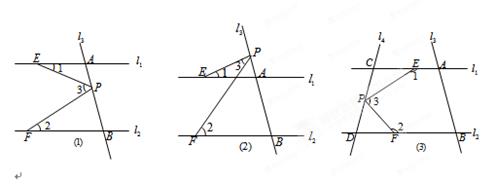
如图,点A、B、C是⊙O上的三点,AB∥OC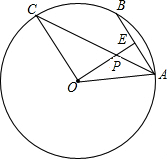
(1)求证:AC平分∠OAB.
(2)过点O作OE⊥AB于点E,交AC于点P.若AB=2,∠AOE=30°,求PE的长.
如图,已知直线l与y轴、x轴交于点A(0,8)、B(6,0)两点,直线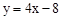 与y轴、直线l分别交于点C、D,求△ACD绕y轴旋转一周所围成几何体的表面积。
与y轴、直线l分别交于点C、D,求△ACD绕y轴旋转一周所围成几何体的表面积。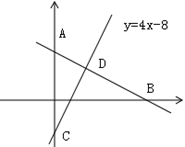
已知:正比例函数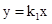 的图象于反比例函数
的图象于反比例函数 的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式。
的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式。
(1)尺规作图:作出⊙O的内接正方形ABCD,使正方形ABCD的对边AD,BC都垂直于EF(见示意图);(说明:不要求写作法,但须保留作图痕迹)
(2)连接EA、EB,求出∠EAD、∠EBC的度数.
已知:如图,正方形ABCD的边长为a,BM,DN分别平分正方形的两个外角,且满足 ∠MAN=45°,连结MC,NC,MN.
(1)填空:与△ABM相似的三角形是△,BM·DN=;(用含a的代数式表示)
(2)求∠MCN的度数;
(3)猜想线段BM,DN和MN之间的数量关系并证明你的结论.