如图所示,A.B两个旅游点从2011年至2015年“清明小长假”期间的旅游人数变化情况分别用实线和虚线表示,请解答以下问题:
(1)B旅游点的旅游人数相对上一年,增长最快的是哪一年?
(2)求A.B两个旅游点从2011年到2015年旅游人数的平均数和方差,并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价;
(3)A旅游点现在的门票价格为每人80元,为保护旅游点环境和游客的安全,A旅游点的最佳接待人数为4万人.A旅游点决定提高门票价格来控制游客数量.已知游客数量y(万人)与门票价格x(元)之间满足函数关系y=5- .若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少元?
.若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少元?
观察下面三行数:
—2, 4, —8, 16, —32, 64,…①
6, —6, 18, —30, 66,…②
,—1, 2, —4, 8, —16, 32,…③(1)第①行数按什么规律排列?
(2)第② ③行数与第①行数分别有什么关系?
(3)取每行的第十个数,计算这三个数的和。25. 出租车司机小李某天下午的营运全是在东西走向的人民大街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6
(1)小李下午出发地记为0,他将最后一名乘客送抵目的地时,小李距下午出车时的出发地有多远?(2)若汽车耗油量为0.41升/千米,这天下午小李共耗油多少升?
小海在实践课中做了一个长方形模型,模型一边长为4a+5b,另一边比它小2a-b,则长方形模型周长为多少?
先化简,后求值(每小题8分,共16分):(1)
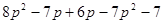 ,其中p=3。
,其中p=3。(2)
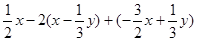 ,其中x=-1,y=2 ;
,其中x=-1,y=2 ;
计算与化简:(1)-3 + 6
(2)

(3)

(4 )

(5)
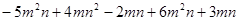
(6)
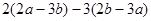
(本题6分)某人去水果批发市场采购苹果,他看中了A、B两家苹果。这两家苹果品质一样,零售价都为6元/千克,批发价各不相同。
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠。
B家的规定如下表:
| 数量范围(千克) |
0~500 |
500以上~1500 |
1500以上~2500 |
2500以上 |
| 价格(元) |
零售价的95% |
零售价的85% |
零售价的75% |
零售价的70% |
【表格说明:批发价格分段计算,如:某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100-1500)】(1)如果他批发600千克苹果,则他在A 家批发需要元,在B家批发需要元;
(2) 如果他批发x千克苹果(1500<x<2000),则他在A 家批发需要元,在B家批发需要元(用含x的代数式表示);
(3) 现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由。