用如图①，②所示的两个直角三角形（部分边长及角的度数在图中已标出），完成以下两个探究问题：
探究一：将以上两个三角形如图③拼接（BC和ED重合），在BC边上有一动点P．
（1）当点P运动到∠CFB的角平分线上时，连接AP，求线段AP的长；
（2）当点P在运动的过程中出现PA=FC时，求∠PAB的度数．
探究二：如图④，将△DEF的顶点D放在△ABC的BC边上的中点处，并以点D为旋转中心旋转△DEF，使△DEF的两直角边与△ABC的两直角边分别交于M、N两点，连接MN．在旋转△DEF的过程中，△AMN的周长是否存在有最小值？若存在，求出它的最小值；若不存在，请说明理由．
如图，已知AB是⊙O的直径，BC⊥AB，连结OC，弦AD∥OC，直线CD交BA的延长线于点E．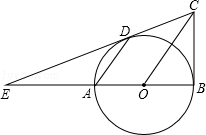
（1）求证：直线CD是⊙O的切线；
（2）若DE=2BC，求AD：OC的值．
如图，函数
的图象与函数
（x＞0）的图象交于A（a，1）、B（1，b）两点．
（1）求函数y2的表达式；
（2）观察图象，比较当x＞0时，y1与y2的大小．
如图所示，在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形．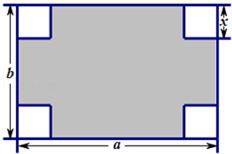
（1）用a，b，x表示纸片剩余部分的面积；
（2）当a=6，b=4，且剪去部分的面积等于剩余部分的面积时，求正方形的边长．
如图，抛物线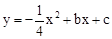
与x轴交于点A（2，0），交y轴于点B（0，
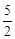）．直线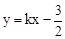
过点A与y轴交于点C，与抛物线的另一个交点是D．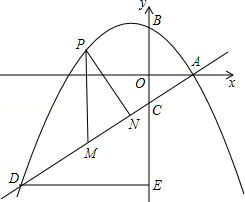
（1）求抛物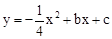线与直线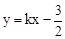的解析式；
（2）设点P是直线AD上方的抛物线上一动点（不与点A、D重合），过点P作 y轴的平行线，交直线AD于点M，作DE⊥y轴于点E．探究：是否存在这样的点P，使四边形PMEC是平行四边形？若存在请求出点P的坐标；若不存在，请说明理由；
（3）在（2）的条件下，作PN⊥AD于点N，设△PMN的周长为l，点P的横坐标为x，求l与x的函数关系式，并求出l的最大值．
如图，在⊙O中，直径AB⊥CD，垂足为E，点M在OC上，AM的延长线交⊙O于点G，交过C的直线于F，∠1=∠2，连结CB与DG交于点N．
（1）求证：CF是⊙O的切线；
（2）求证：△ACM∽△DCN；
（3）若点M是CO的中点，⊙O的半径为4，cos∠BOC=
，求BN的长．