如图，在平面直角坐标系中，△ABC的顶点A在x轴负半轴上，顶点C在x轴正半轴上，顶点B在第一象限，过点B作BD⊥y轴于点D，线段OA，OC的长是一元二次方程x2﹣12x+36=0的两根，BC=4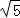
，∠BAC=45°．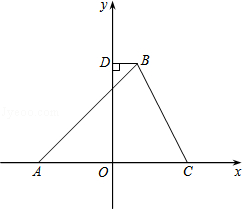
（1）求点A，C的坐标；
（2）反比例函数y=
的图象经过点B，求k的值；
（3）在y轴上是否存在点P，使以P，B，D为顶点的三角形与以P，O，A为顶点的三角形相似？若存在，请写出满足条件的点P的个数，并直接写出其中两个点P的坐标；若不存在，请说明理由．
如图，从A地到B地的公路需经过C地，图中AC=10千米，∠CAB=25°，∠CBA=37°．因城市规划的需要，将在A、B两地之间修建一条笔直的公路．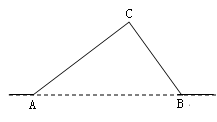
（1）求改直后的公路AB的长；
（2）问公路改直后该段路程比原来缩短了多少千米？（精确到0．1）
（sin25°≈0．42，cos25°≈0．91,sin37°≈0．60，tan37°≈0．75）
已知：如图，在平行四边形ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．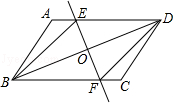
（1）求证：OE=OF．
（2）当∠DOE等于度时，四边形BFDE为菱形。（直接填写答案即可）
先化简，再求值：（x+1）（x﹣1）﹣x（x﹣2），其中x=
．
如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．
（1）求线段CD的长；
（2）设△CPQ的面积为S，求S与t之间的函数关系式，并确定在运动过程中是否存在某一时刻t，使得S△CPQ：S△ABC=9：100？若存在，求出t的值；若不存在，则说明理由．
（3）是否存在某一时刻t，使得△CPQ为等腰三角形？若存在，求出所有满足条件的t的值；若不存在，则说明理由．
如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB于点F，连接BE．
（1）求证：AC平分∠DAB；
（2）求证：PC=PF；
（3）若tan∠ABC=
，AB=14，求线段PC的长．