阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是减函数.
例题:证明函数f(x)= (x>0)是减函数.
(x>0)是减函数.
证明:假设x1<x2,且x1>0,x2>0
f(x1)﹣f(x2)= ﹣
﹣ =
= =
=
∵x1<x2,且x1>0,x2>0
∴x2﹣x1>0,x1x2>0
∴ >0,即f(x1)﹣f(x2)>0
>0,即f(x1)﹣f(x2)>0
∴f(x1)>f(x2)
∴函数f(x)= (x>0)是减函数.
(x>0)是减函数.
根据以上材料,解答下面的问题:
(1)函数f(x)= (x>0),f(1)=
(x>0),f(1)= =1,f(2)=
=1,f(2)= =
= .
.
计算:f(3)= ,f(4)= ,猜想f(x)= (x>0)是 函数(填“增”或“减”);
(x>0)是 函数(填“增”或“减”);
(2)请仿照材料中的例题证明你的猜想.
如图,已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC.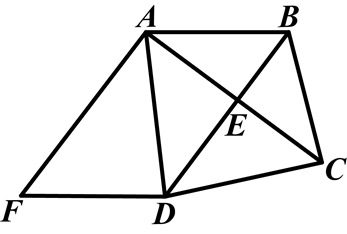
(1)证明ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.
在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),则根据勾股定理,得a2+b2=c2.若△ABC不是直角三角形,如图(2)和(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.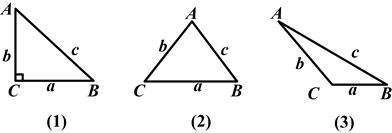
小明、小华在一栋电梯楼前感慨楼房真高.小明说:“这楼起码20层!”小华却不以为然:“20层?我看没有,数数就知道了!”小明说:“有本事,你不用数也能明白!”小华想了想说:“没问题!让我们来量一量吧!”小明、小华在楼体两侧各选一点,分别为A、B,测量数据如图,其中矩形CDEF表示楼体,AB=150米,CD=10米,∠A=30°,∠B=45°(A、C、D、B四点在同一直线上).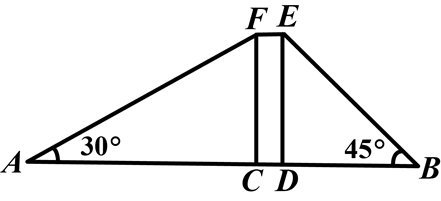
(1)问:楼高多少米?
(2)若每层楼按3米计算,你支持小明还是小华的观点呢?请说明理由.(参考数据: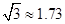 ,
,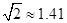 ,
,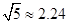 )
)
如图,将长方形沿直线AE折叠,使顶点D恰好落在BC边上F点处,已知CE=3cm,AB=8cm,求图中阴影部分的面积.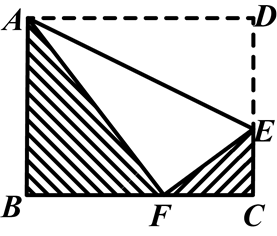
已知:如图所示,AC=4,BC=3,AD=13,DB=12,∠C=90°.
求证:AB⊥BD.