小明、小华在一栋电梯楼前感慨楼房真高.小明说:“这楼起码20层!”小华却不以为然:“20层?我看没有,数数就知道了!”小明说:“有本事,你不用数也能明白!”小华想了想说:“没问题!让我们来量一量吧!”小明、小华在楼体两侧各选一点,分别为A、B,测量数据如图,其中矩形CDEF表示楼体,AB=150米,CD=10米,∠A=30°,∠B=45°(A、C、D、B四点在同一直线上).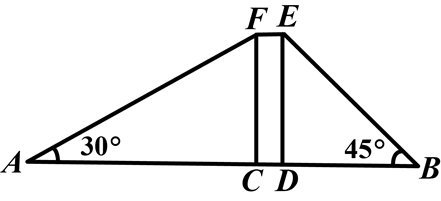
(1)问:楼高多少米?
(2)若每层楼按3米计算,你支持小明还是小华的观点呢?请说明理由.(参考数据: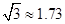 ,
,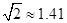 ,
,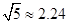 )
)
已知:如图,在△ABC中,AB=AC,D为BC上的一点,DA平分∠EDC,且∠E=∠B.求证:△ADE≌△ADC.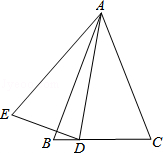
如图,在等腰直角△ABC中,∠ABC=90°,AB=BC=4,P为AC中点,E为AB边上一动点,F为BC边上一动点,且满足条件∠EPF=45°,记四边形PEBF的面积为S1;
(1)求证:∠APE=∠CFP;
(2)记△CPF的面积为S2,CF=x,y= .
.
①求y关于x的函数解析式和自变量的取值范围,并求y的最大值.
②在图中作四边形PEBF关于AC的对称图形,若它们关于点P中心对称,求y的值.
对于任意的实数x,记f(x)= .
.
例如:f(1)= =
=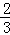 ,f(﹣2)=
,f(﹣2)= =
=
(1)计算f(2),f(-3)的值;
(2)试猜想f(x)+f(﹣x)的值,并说明理由;
(3)计算f(﹣2014)+f(﹣2013)+…+f(﹣1)+f(0)+f(1)+…+f(2013)+f(2014).
如图,游客从某旅游景区的景点A处下山至C处有两种路径,一中是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为45m/min.乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,两人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,经测量,∠CAB=45°,∠CBA=105°.(参考数据: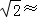 1.4,1.7)
1.4,1.7)
(1)求索道AB的长;
(2)为乙的步行速度.
如图,已知AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于点D.
(1)证明:直线PB是⊙O的切线;
(2)若BD=2PA,OA=3,PA=4,求BC的长.