2015年5月,某校组织了以“德润书香”为主题的电子小报制作比赛,评分结果只有60,70,80,90,100五种,现从中随机抽取部分作品,对其份数和成绩进行整理,制成如下两幅不完整的统计图:
根据以上信息,解答下列问题:
(1)求本次抽取了多少份作品,并补全两幅统计图;
(2)已知该校收到参赛作品共900份,比赛成绩达到90分以上(含90分)的为优秀作品,据此估计该校参赛作品中,优秀作品有多少份?
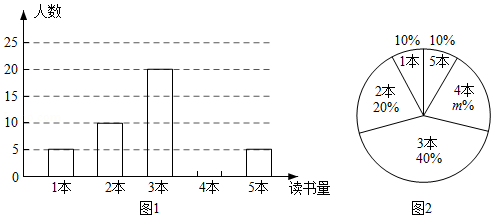
为迎接中国共产党建党100周年,某校开展了以“不忘初心,缅怀先烈”为主题的读书活动,学校政教处对本校七年级学生五月份“阅读该主题相关书籍的读书量”(下面简称“读书量” 进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,如图所示:
(1)补全下面图1的统计图;
(2)本次所抽取学生五月份“读书量”的众数为 ;
(3)已知该校七年级有1200名学生,请你估计该校七年级学生中,五月份“读书量”不少于4本的学生人数.
如今,柳州螺蛳粉已经成为名副其实的“国民小吃”,螺蛳粉小镇对 、 两种品牌的螺蛳粉举行展销活动.若购买20箱 品牌螺蛳粉和30箱 品牌螺蛳粉共需要4400元,购买10箱 品牌螺蛳粉和40箱 品牌螺蛳粉则需要4200元.
(1)求 、 品牌螺蛳粉每箱售价各为多少元?
(2)小李计划购买 、 品牌螺蛳粉共100箱,预算总费用不超过9200元,则 品牌螺蛳粉最多购买多少箱?
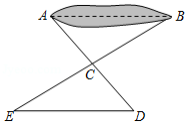
如图,有一池塘,要测池塘两端 、 的距离,可先在平地上取一个点 ,从点 不经过池塘可以直接到达点 和 ,连接 并延长到点 ,使 ,连接 并延长到点 ,使 ,连接 ,那么量出 的长就是 、 的距离,为什么?请结合解题过程,完成本题的证明.
证明:在 和 中,
,
,
.
解分式方程: .
计算: .