在平面直角坐标系中,点
的坐标是(0,3),点
在
轴上,将
绕点
逆时针旋转90°得到
,点
、
的对应点分别是点
、
.
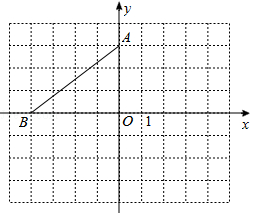
(1)若点
的坐标是
,请在图中画出
,并写出点
、
的坐标.
(2)当点
落在
轴的上方时,试写出一个符合条件的点
的坐标.
如图所示,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).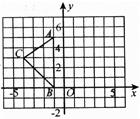
求出△ABC的面积;
在图中作出△ABC关于y轴的对称图形△A1B1C1;
写出点A1,B1,C1的坐标.
如图,已知AD⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°,那么BC⊥AB,说明理由。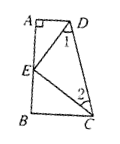
如图所示,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1,2).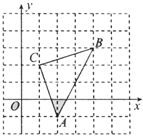
写出点A、B的坐标;
将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,分别写出△A′B′C′的三个顶点坐标;
如图所示,将△ABC沿EF折叠,使点C落到点C′处,试探求∠1,∠2与∠C的关系.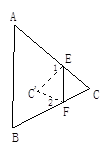
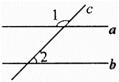
如图所示,直线a,b被直线c所截,且∠1+∠2=180°,直线a与直线b平行吗?为什
么?