小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.
一辆货车在A处加满油后匀速行驶,下表记录的是货车一次加满油后油箱内余油量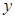 (升)与行驶时间
(升)与行驶时间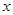 (时)之间的关系:
(时)之间的关系:
行驶时间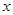 (时) (时) |
0 |
1 |
2 |
2.5 |
余油量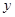 (升) (升) |
100 |
80 |
60 |
50 |
求
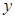 与
与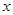 之间的函数关系式
之间的函数关系式求货车行驶4.2小时到达B处时油箱内的余油量
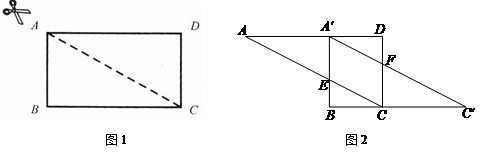
将图1中的矩形ABCD沿对角线AC剪开,再把△ABC沿着AD方向平移,得到图2中的△A′BC′写出图2中的两对全等的三角形(不能添加辅助线和字母,△C′BA′
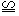 △ADC除外);
△ADC除外);选择一对加以证明.
学校以1班学生的地理测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成两幅统计图,结合图中信息填空:D级学生的人数占全班人数的百分比为▲
扇形统计图中C级所在扇形圆心角度数为▲
该班学生地理测试成绩的中位数落在▲级内
若该校共有1500人,则估计该校地理成绩得A级的学生约有▲人.

从2开始,将连续的偶数相加,和的情况有如下规律:
2=1×2,
2+4=6=2×3,
2+4+6=12=3×4,
2+4+6+8=20=4×5,
2+4+6+8+10=30=5×6,
2+4+6+8+10+12=42=6×7,
……
按此规律,从2开始连续2011个偶数相加,其和是多少?
从2开始连续n个偶数相加,和是多少
1000+1002+1004+1006+……+2012的和是多少?
学校组织同学到博物馆参观,小明因事没有和同学同时出发,于是准备在学校门口搭乘出租车赶去与同学们会合,出租车的收费标准是:起步价为6元,3千米后每千米收1.2元,不足1千米的按1千米计算.请你回答下列问题小明乘车3.8千米,应付费_________元
小明乘车X(X是大于3的整数)千米,应付费多少钱?
小明身上仅有10元钱,乘出租车到距学校7千米远的博物馆的车费够不够?请说明理由.