如图①，半径为R，圆心角为n°的扇形面积是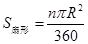
，由弧长l=
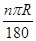，得=
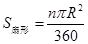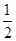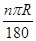••R=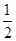lR．通过观察，我们发现S扇形=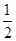lR类似于S三角形=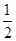×底×高．
类比扇形，我们探索扇环（如图②，两个同心圆围成的圆环被扇形截得的一部分交作扇环）的面积公式及其应用．
（1）设扇环的面积为S扇环，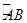
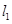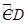的长为
，
的长为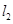
，线段AD的长为h（即两个同心圆半径R与r的差）．类比S梯形=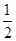×（上底+下底）×高，用含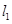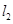，，h的代数式表示S扇环，并证明；
（2）用一段长为40m的篱笆围成一个如图②所示的扇环形花园，线段AD的长h为多少时，花园的面积最大，最大面积是多少？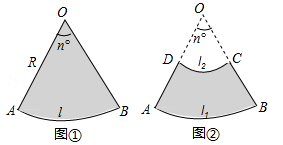
建设北路街道改建工程指挥部，要对该路段工程进行招标，接到了甲、乙两个工程队的投标书.从投标书中得知：甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的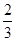
；若由甲队先做10天，则剩下的工程由甲、乙两队合作30天就可以完成.
（1）求甲、乙两队单独完成这项工程各需多少天？
（2）已知甲队每天的施工费用为0.84万元，乙队每天的施工费用为0.56万元.工程预算的施工费用为50万元.为缩短工期以减少对住户的影响，拟安排甲、乙两队合作完成这项工程，则工程预算的施工费用是否够用？若不够用，需追加预算多少万元？请给出你的判断并说明理由.
如图，Rt△ABO的顶点A是双曲线
与直线
在第二象限内的交点，AB⊥
轴于点B，且
.
（1）求这两个函数的表达式；
（2）求直线与双曲线的两个交点A、C的坐标；
（3）求△AOC的面积.
某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元。为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施。经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件。
（1）若商场平均每天要盈利1200元，每件衬衫应降价多少元？
（2）若商场为增加效益最大化，求每件衬衫应降价多少元时，商场平均每天盈利最多？每天最多盈利多少元？
如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE. 已知∠BAC=30º，EF⊥AB，垂足为F，连结DF．
（1）试说明AC=EF；
（2）求证：四边形ADFE是平行四边形。
在一次数学活动课上，李老师带领学生去测教学楼的高度。在阳光下，测得身高1.65米的黄丽同学BC的影长BA为1.1米，与此同时，测得教学楼DE的影长DF为12.1米.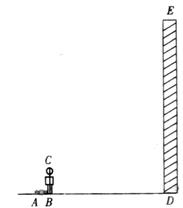
（1）请你在图中画出此时教学楼DE在阳光下的投影DF；
（2）请你根据已测得的数据，求出教学楼DE的高度（精确到0.1米）.