已知数列{an}各项均为正数,其前n项和为Sn,且满足4Sn=(an+1)2.
(1)求{an}的通项公式;
(2)设bn=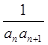 ,求数列{bn}的前n项和为Tn
,求数列{bn}的前n项和为Tn
(本小题满分14分)
设{an}是正数组成的数列,其前n项和为Sn,并且对于所有的n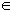 N+,都有
N+,都有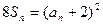 。
。
(1)写出数列{an}的前3项;
(2)求数列{an}的通项公式(写出推证过程);
(3)设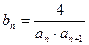 ,
,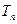 是数列{bn}的前n项和,求使得
是数列{bn}的前n项和,求使得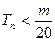 对所有n
对所有n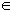 N+都成立的最小正整数
N+都成立的最小正整数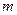 的值。
的值。
(本小题满分14分)
一农民有基本农田2亩,根据往年经验,若种水稻,则每季每亩产量为400公斤;若种花生,则每季每亩产量为100公斤。但水稻成本较高,每季每亩240元,而花生只需80元,且花生每公斤5元,稻米每公斤卖3元。现该农民手头有400元,两种作物各种多少,才能获得最大收益?
(本小题满分14分)
在△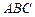 中,已知a、b、
中,已知a、b、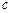 分别是三内角
分别是三内角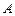 、
、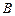 、
、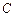 所对应的边长,且
所对应的边长,且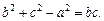
(1)求角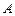 的大小;
的大小;
(2)若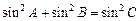 ,试判断△ABC的形状并求角
,试判断△ABC的形状并求角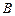 的大小.
的大小.
设函数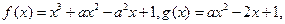 其中实数
其中实数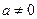 .
.
(1)当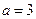 时,求函数
时,求函数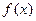 的单调区间;
的单调区间;
(2)当函数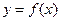 与
与 的图象只有一个公共点且
的图象只有一个公共点且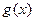 存在最小值时,
存在最小值时,
记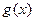 的最小值为
的最小值为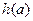 ,求函数
,求函数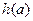 的值域;
的值域;
(3)若函数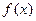 与
与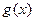 在区间
在区间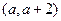 内均为增函数,求实数
内均为增函数,求实数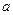 的取值范围.
的取值范围.
某地区有100户农民,都从事水产养殖。据了解,平均每户的年收入为3万元。为了调整产业结构,当地政府决定动员部分农民从事水产加工。据估计,如果能动员 户农民从事水产加工,那么剩下的继续从事水产养殖的农民平均每户的年收入有望提高
户农民从事水产加工,那么剩下的继续从事水产养殖的农民平均每户的年收入有望提高 ,而从事水产加工的农民平均每户的年收入将为
,而从事水产加工的农民平均每户的年收入将为 万元.
万元.
(1)在动员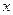 户农民从事水产加工后,要使从事水产养殖的农民的总年收入不低于动员前从事水产养殖的农民的总年收入,求
户农民从事水产加工后,要使从事水产养殖的农民的总年收入不低于动员前从事水产养殖的农民的总年收入,求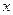 的取值范围;
的取值范围;
(2)若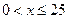 ,要使这100户农民中从事水产加工的农民的总年收入始终不高于从事水产养殖的农民的总年收入,求
,要使这100户农民中从事水产加工的农民的总年收入始终不高于从事水产养殖的农民的总年收入,求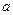 的最大值.
的最大值.