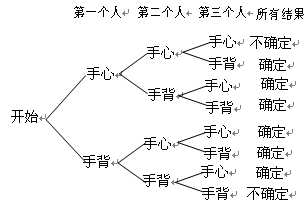
如图,抛物线
与
轴交于
两点,顶点
关于
轴的对称点是
.

(1)求抛物线的解析式;
(2)若直线
与此抛物线的另一个交点为
,求
的面积;
(3)是否存在过
两点的抛物线,其顶点
关于
轴的对称点为
,使得四边形
为正方形?若存在,求出此抛物线的解析式;若不存在,请说明理由.
计算:(1)2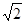 +
+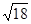 -4
-4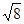
如图,抛物线y=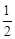 x2+bx+c与y轴交于点C,与x轴相交于A,B两点,点A的坐标为(2,0),点C的坐标为(0,―4).
x2+bx+c与y轴交于点C,与x轴相交于A,B两点,点A的坐标为(2,0),点C的坐标为(0,―4).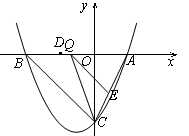
(1)求抛物线的解析式;
(2)点Q是线段OB上的动点,过点Q作QE//BC,交AC于点E,连接CQ,设OQ=m,当△CQE的面积最大时,求m的值,并写出点Q的坐标.
(3)若平行于x轴的动直线,与该抛物线交于点P,与直线BC交于点F,D的坐标为(-2,0),则是否存在这样的直线l,使OD=DF?若存在,求出点P的坐标;若不存在,请说明理由.
如图,在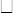 ABCD中,AE∶EB=2∶3.
ABCD中,AE∶EB=2∶3.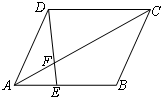
(1)求△AEF和△CDF的周长比;
(2)若S△AEF=8cm2,求S△CDF.
某宾馆有50个房间供游客居住,当每个房间的定价为每天180元时,房间会全部住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.房价定为多少时,宾馆利润最大?
活动课,小赵、小钱和小孙三同学准备打羽毛球,他们约定用“手心手背”的方式来确定哪两个人先上场,三人同时出一只手为一个回合.若所出三只手中,恰有两只手的手心向上或手背向上的这两个人先上场;若所出三只手均为手心向上或手背向上,属于不能确定.求一个回合能确定两人先上场的概率.