如图，已知Rt△ABC中，∠C=90°，AC=8，BC=6，点P以每秒1个单位的速度从A向C运动，同时点Q以每秒2个单位的速度从A→B→C方向运动，它们到C点后都停止运动，设点P，Q运动的时间为t秒．
（1）在运动过程中，求P，Q两点间距离的最大值；
（2）经过t秒的运动，求△ABC被直线PQ扫过的面积S与时间t的函数关系式；
（3）P，Q两点在运动过程中，是否存在时间t，使得△PQC为等腰三角形？若存在，求出此时的t值；若不存在，请说明理由（
≈2．24，结果保留一位小数）
如图，已知在等腰直角三角形△DBC中，∠BDC=90°，BF平分∠DBC，与CD相交于点F，延长BD到A，使DA=DF，
（1）试说明：△FBD≌△ACD；
（2）延长BF交AC于E，且BE⊥AC，试说明：CE＝
如图，是一次函数y=kx+b的图象．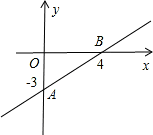
（1）求这个一次函数的解析式？
（2）试判断点P（1，-1）是否在这个一次函数的图象上？
（3）求原点O到直线AB的距离．
已知平面直角坐标系中有一点M（m-1，2m+3）
（1）当m为何值时，点M到x轴的距离为1？
（2）当m为何值时，点M到y轴的距离为2？
已知，如图，四边形ABCD，∠A=∠B=Rt∠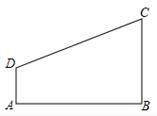
（1）用直尺和圆规，在线段AB上找一点E，使得EC=ED，连接EC，ED（不写作法，保留作图痕迹）
（2）在（1）的图形中，若∠ADE=∠BEC，且CE=3，BC=
，求AD的长．
解不等式组：
并把解集在数轴上表示出来。