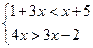已知抛物线 与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(﹣1,0),点C的坐标是(0,﹣3).
与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(﹣1,0),点C的坐标是(0,﹣3).
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式和∠ABC的度数;
(3)P为线段BC上一点,连接AC,AP,若∠ACB=∠PAB,求点P的坐标.
已知Rt△ABC和Rt△EBC, °。以边AC上的点O为圆心、OA为半径的⊙O与EC相切,D为切点,AD//BC。
°。以边AC上的点O为圆心、OA为半径的⊙O与EC相切,D为切点,AD//BC。
(1)用尺规确定并标出圆心O;(不写做法和证明,保留作图痕迹)
(2)求证:
(3)若AD=1, ,求BC的长。
,求BC的长。
某市有A,B,C,D四个区。A区2003年销售了商品房2千套,从2003年到2007年销售套数(y)逐年(x)呈直线上升,A区销售套数2009年与2006年相等,2007年与2008年相等(如图①所示);2009年四个区的销售情况如图②所示,且D区销售了2千套
(1)求图②中D区所对扇形的圆心角的度数及2009年A区的销售套数;
(2)求2008年A区的销售套数
如图,华庆号船位于航海图上平面直角坐标系中的点A(10,2)处时,点C、海岛B的位置在y轴上,且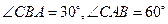

(1)求这时船A与海岛B之间的距离;
(2)若海岛B周围16海里内有海礁,华庆号船继续沿AC向C航行有无触礁危险?请说明理由
在梯形ABCD中,AD//BC,AB=CD,E为AD中点
(1)求证:△ABE≌△DCE
(2)若BE平分 ,且AD=10,求AB的长
,且AD=10,求AB的长
解不等式组: